Déterminer si un nombre est premier

Divisibilité

Soit a et b deux nombres entiers naturels.
On dit que b est un diviseur de a s'il existe un nombre entier naturel q tel que a = b × q.
On dit aussi que a est un multiple de b, ou que a est divisible par b.
Exemple : 72 est divisible par 8 (et par 9) car 72 = 8 × 9.

Nombres premiers

Un nombre entier naturel (supérieur ou égal à 2) est un nombre premier s'il admet exactement 2 diviseurs : 1 et lui-même.
Exemple : 2, 3, 5, 7, 11, 13, 17, 19 … sont des nombres premiers. Il en existe une infinité.

Remarque

Pour déterminer si un nombre entier naturel n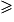 supérieur ou égal

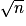2 est un nombre premier, on doit chercher un diviseur de n parmi les nombres premiers successifs (2, 3, 5, 7, 11 …) jusqu'à la valeur $\sqrt{n}$ .
En effet, si n n'admet aucun diviseur parmi les nombres premiers successifs jusqu'à la valeur 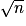$\sqrt{n}$ , il n'en admettra pas non plus entre 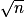$\sqrt{n}$ et n car les diviseurs d'un nombre vont par paires : l'un compris entre 2 et 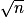$\sqrt{n}$ , et l'autre compris entre 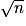$\sqrt{n}$ et n.
Si n n'admet aucun diviseur parmi les nombres premiers successifs jusqu'à la valeur 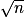$\sqrt{n}$ , c'est donc un nombre premier.

Crible d'Ératosthène

Dans le crible d'Ératosthène, qui contient les nombres de 1 à 100, on a rayé successivement les multiples de 2, ceux de 3, ceux de 5 et ceux de 7 (11² > 100), pour obtenir la liste des nombres premiers inférieurs à 100.
1 est considéré comme n'étant pas un nombre premier.

Exercice n°1

Parmi les nombres suivants, lequel est un nombre premier ?

Cochez la bonne réponse.

813

821

837

8 + 1 + 3 = 12, qui est divisible par 3, donc 813 est divisible par 3 (813 = 3 × 271) et n'est pas un nombre premier.
8 + 3 + 7 = 18, qui est divisible par 9, donc 837 est divisible par 9 (837 = 9 × 93) et n'est pas un nombre premier.

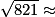$\sqrt{821}\approx$ 28,7, donc il faut chercher un éventuel diviseur premier de 821 parmi la liste des nombres premiers compris entre 2 et 28.
D'après le crible d'Ératosthène, il s'agit des nombres 2, 3, 5, 7, 11, 13, 17, 19 et 23.
Après calculs, aucun de ces nombres ne divise 821, donc c'est un nombre premier.

Exercice n°2

Le nombre 991 est un nombre premier.

Cochez la bonne réponse.

Vrai

Faux

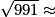$\sqrt{991}\approx$ 31,5 donc il faut chercher un éventuel diviseur premier de 991 parmi la liste des nombres premiers compris entre 2 et 31.
D'après le crible d'Ératosthène, il s'agit des nombres 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 et 31.
Après calculs, aucun de ces nombres ne divise 991, donc c'est un nombre premier.
L'affirmation est donc vraie.

Exercice n°3

Le nombre 37 est un nombre premier.

Cochez la bonne réponse.

Vrai

Faux

Vrai. 37 n'est pas divisible par 2, 3 et 5 (7² > 37), donc c'est un nombre premier.

Aussi, en observant le crible d'Ératosthène, on s'aperçoit que 37 est un nombre premier.

Exercice n°4

Le nombre 91 est un nombre premier.

Cochez la bonne réponse.

Vrai

Faux

Faux. 91 n'est pas divisible par 2, 3 et 5, mais il est divisible par 7 car 91 = 7 × 13. 91 n'est donc pas un nombre premier.

Aussi, en observant le crible d'Ératosthène, on s'aperçoit que 91 n'est pas un nombre premier.