Résolvons l'inéquation : –8x – 5  3.
3.
 3.
3.• On transpose le nombre 5 d'un membre à l'autre de l'inégalité, en ajoutant son opposé (+5) aux deux membres.
–8x 3 + 5 ou –8x
3 + 5 ou –8x  8
8
–8x
 3 + 5 ou –8x
3 + 5 ou –8x  8
8• Pour isoler x, on divise par 8 les deux membres de l'inégalité.
On obtient : –x 1.
1.
On obtient : –x
 1.
1.• Pour obtenir x à partir de –x, il faut changer le sens de l'inégalité.
Donc : x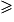 –1.
–1.
Donc : x
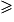 –1.
–1.• On peut représenter l'ensemble des solutions de l'inéquation sur une droite (partie non hachurée).
 |
Remarque : quand l'inéquation est du type ax + b < cx + d, on regroupe les termes en x, d'un côté ; les termes sans x, de l'autre.
On est ramené au cas précédent.
7x + 9 < 5 + 5x
7x – 5x < 5 – 9
x < – 2
On est ramené au cas précédent.
7x + 9 < 5 + 5x
7x – 5x < 5 – 9
x < – 2
Exercice n°1
Simplifie l'inéquation, puis résous-la.
1. L'inéquation 4x − 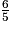 < 7x peut s'écrire :
< 7x peut s'écrire :
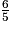 < 7x peut s'écrire :
< 7x peut s'écrire : Cochez la bonne réponse.
| ||
| ||
| ||
|
2. L'inéquation admet pour solutions :
Sélectionnez la (ou les) bonne(s) réponse(s) dans le texte.
en violet
-1 -0,4 -0,1 0 1 4
1. 4x − 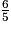 < 7x
< 7x
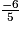 < 7x − 4x
< 7x − 4x
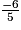 < 3x
< 3x
Donc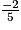 < x.
< x.
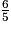 < 7x
< 7x 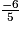 < 7x − 4x
< 7x − 4x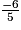 < 3x
< 3x Donc
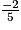 < x.
< x. 2. Les solutions sont donc les nombres strictement plus grands que 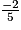 ou -0,4.
ou -0,4.
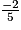 ou -0,4.
ou -0,4.Exercice n°2
Soit l'inégalité (I) : 2x + 15 < x − 6.
Parmi les inégalités citées ci-dessous, trouve celle qui a la même signification, pour le nombre x, que l'inégalité (I).
Parmi les inégalités citées ci-dessous, trouve celle qui a la même signification, pour le nombre x, que l'inégalité (I).
Cochez la bonne réponse.
| ||
| ||
| ||
|
Il faut résoudre chaque inéquation.
Les solutions sont : x < -15 pour l'inéquation (I).
Les solutions sont : x < -15 pour l'inéquation (I).
Or, les équations proposées se simplifient ainsi :
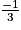 x < -5 = x > 15
x < -5 = x > 15
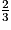 x < 10 = x < 15
x < 10 = x < 15
x + 1 <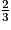 x − 4 = x < -15
x − 4 = x < -15
x −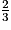 x < -7 = x < -21
x < -7 = x < -21
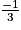 x < -5 = x > 15
x < -5 = x > 15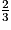 x < 10 = x < 15
x < 10 = x < 15x + 1 <
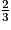 x − 4 = x < -15
x − 4 = x < -15x −
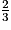 x < -7 = x < -21
x < -7 = x < -21Exercice n°3
On considère le système d'inéquations suivant : 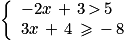
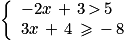
Quels sont les nombres qui sont solution de ce système ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
|
Résous chacune des deux inéquations et trouve un encadrement de x.
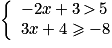
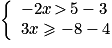
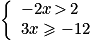
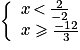
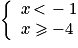
Les nombres x solutions du système sont tels que − 4
 x < −1.
x < −1.
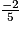
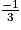 x < -5
x < -5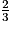 x < 10
x < 10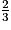 x − 4
x − 4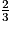 x < -7
x < -7
