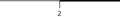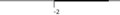Exemple 1
Résolvons l'inéquation : 5x < 15.
• Pour isoler x, on divise par 5 les deux membres de l'inégalité.
Comme 5 est un nombre positif, le sens de l'inégalité ne change pas.
< 
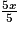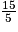donc x < 3.• On peut représenter l'ensemble des solutions sur une droite graduée (partie non hachurée).
 |
Exemple 2
Résolvons maintenant l'équation : –8x < –16.
• Pour isoler x, on divise par 8 les deux membres de l'inégalité. On obtient : –x < –2.
Pour obtenir x à partir de –x, il faut changer le sens de l'inégalité. Donc : x > 2.
• On peut représenter l'ensemble des solutions sur une droite graduée (partie non hachurée).
 |
Exercice n°1
On veut résoudre l'inéquation : -4 < -2x.
Complète le raisonnement.
Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
1. On isole x en divisant les deux membres de l'inégalité par .
Comme est négatif, le sens de l'inégalité est inversé.
Comme est négatif, le sens de l'inégalité est inversé.
2. On en déduit : > x, ou encore : x < .
On a : -4 < -2x.
Pour isoler x, il faut diviser par -2. Quand on divise les deux membres par un nombre négatif, on change le sens de l'inégalité :
> 
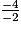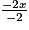
Pour isoler x, il faut diviser par -2. Quand on divise les deux membres par un nombre négatif, on change le sens de l'inégalité :
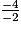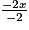
> Exercice n°2
L'ensemble des solutions est représenté par la partie en rouge non hachurée.
Quelle est la représentation graphique qui correspond à l'ensemble des solutions de l'inéquation : -3x
9 ?
Quelle est la représentation graphique qui correspond à l'ensemble des solutions de l'inéquation : -3x
9 ?
| ||
| Représentation 1 |
| ||
| Représentation 2 |
| ||
| Représentation 3 |
• Pour isoler x, il faut diviser les deux membres par -3. On change donc le sens de l'inégalité :
x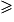
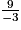, soit x 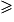-3.
x
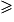
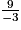, soit x 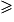-3. • Attention au sens du crochet.
Exercice n°3
Coche la bonne réponse.
Si a < − 2, alors 5a < − 17.
Cochez la bonne réponse.
| ||
|
−3 est une des solutions de l'inéquation − 4x + 7 < 10.
Cochez la bonne réponse.
| ||
|
L'inéquation −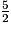
x <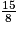 
a pour solution 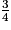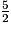x > −
.
x < 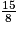a pour solution x > −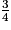. Cochez la bonne réponse.
| ||
|
Quand tu multiplies une inégalité par un nombre négatif, pense à changer le sens de l'inégalité.
• 5 est un nombre positif, donc on conserve le sens de l'inégalité. Par contre, 5 × (− 2) = − 10 et non − 17.
• Calcule − 4x + 7 pour x = − 3, tu trouves − 4(− 3) + 7 = 12 + 7 = 19. Or 19 > 10, donc − 3 n'est pas solution.
• Divise l'inégalité par −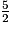
qui est négatif : ce nombre est négatif.
Tu obtiens : x >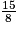
÷ (−
)
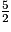x >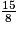
× (−
)
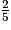x > −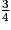
.
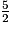qui est négatif : ce nombre est négatif.Tu obtiens : x >
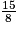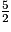÷ (−)x >
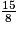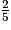× (−)x > −
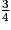.Exercice n°4
Quelle est la représentation qui correspond à la solution de l'inéquation −3x + 7 > 4x − 7 ?
|
|
|
Résous l'inéquation : si tu divises par un nombre négatif, change le sens de l'inégalité.
• La résolution de l'inéquation donne :
− 3x + 7 > 4x − 7
− 3x − 4x > − 7 − 7
−7x > − 14
x <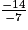
x < 2.
− 3x + 7 > 4x − 7
− 3x − 4x > − 7 − 7
−7x > − 14
x <
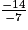
x < 2.
• La représentation qui convient est donc :
 |
