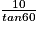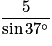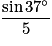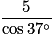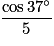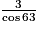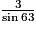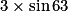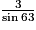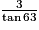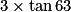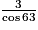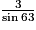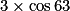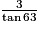Si on connaît un angle et un côté d'un triangle rectangle, on peut calculer les autres côtés.
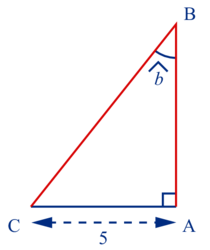
Soit ABC un triangle rectangle en A.
On donne :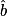 = 30° et AC = 5.
= 30° et AC = 5.
On veut calculer BC et AB.
[AC] étant le côté opposé à l'angle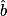 , on peut calculer BC avec
, on peut calculer BC avec 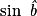 ; puis calculer AB avec
; puis calculer AB avec 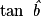
On donne :
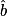 = 30° et AC = 5.
= 30° et AC = 5.On veut calculer BC et AB.
[AC] étant le côté opposé à l'angle
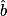 , on peut calculer BC avec
, on peut calculer BC avec 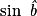 ; puis calculer AB avec
; puis calculer AB avec 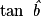
 |
• Calcul de BC :
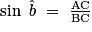 ; donc
; donc 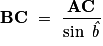
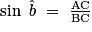 ; donc
; donc 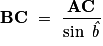
BC = 5 ÷ sin 30° = 5 ÷ 0,5 = 10
• Calcul de AB :
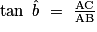 ; donc
; donc 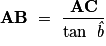
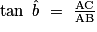 ; donc
; donc 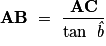
AB = 5 ÷ tan 30° = 8,66
Exercice n°1
Soit un triangle MNP rectangle en M. L'angle 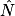 mesure 20° et NP vaut 9.
mesure 20° et NP vaut 9.
On veut calculer MP et MN (valeurs arrondies au centième).
Complète le raisonnement.
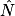 mesure 20° et NP vaut 9.
mesure 20° et NP vaut 9.On veut calculer MP et MN (valeurs arrondies au centième).
Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
1. On connaît NP, l' de MNP.
2. Pour calculer MP, le côté à l'angle 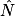 , on utilise le de cet angle.
, on utilise le de cet angle.
On obtient : MP = .
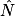 , on utilise le de cet angle.
, on utilise le de cet angle.On obtient : MP = .
3. Pour calculer MN, le côté à l'angle 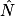 , on utilise le de cet angle.
, on utilise le de cet angle.
On obtient : MN = .
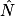 , on utilise le de cet angle.
, on utilise le de cet angle.On obtient : MN = .
2. sin 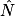 =
= 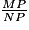 ; sin 20° =
; sin 20° = 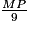 .
.
Donc MP = 9 × sin 20°.
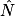 =
= 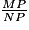 ; sin 20° =
; sin 20° = 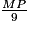 .
. Donc MP = 9 × sin 20°.
3. cos 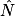 =
= 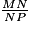 ; cos 20° =
; cos 20° = 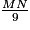 .
.
Donc MN = 9 × cos 20°.
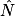 =
= 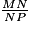 ; cos 20° =
; cos 20° = 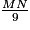 .
.Donc MN = 9 × cos 20°.
Exercice n°2
ABC est un triangle rectangle en A tel que 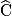 = 37° et AC = 5.
= 37° et AC = 5.
La longueur BC est égale à :
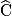 = 37° et AC = 5.
= 37° et AC = 5.La longueur BC est égale à :
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
| ||
|
cos 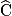 =
= 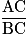 donc BC =
donc BC = 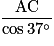 =
= 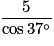 .
.
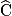 =
= 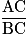 donc BC =
donc BC = 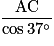 =
= 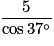 .
.Exercice n°3
ABC est un triangle rectangle en C tel que AC = 3 et 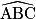 = 63°. Alors : (l'unité de longueur est le cm)
= 63°. Alors : (l'unité de longueur est le cm)
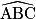 = 63°. Alors : (l'unité de longueur est le cm)
= 63°. Alors : (l'unité de longueur est le cm) Cochez la bonne réponse.
| ||
| ||
|
Dans le même triangle :
Cochez la bonne réponse.
| ||
| ||
|
ABC est un triangle rectangle en C tel que BC = 3 et 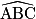 = 63°. Alors :
= 63°. Alors :
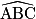 = 63°. Alors :
= 63°. Alors : Cochez la bonne réponse.
| ||
| ||
|
Dans le même triangle :
Cochez la bonne réponse.
| ||
| ||
|
Exercice n°4
Soit un triangle RST rectangle en R.
L'angle en S mesure 60° et RT vaut 10.
On veut calculer RS.
L'angle en S mesure 60° et RT vaut 10.
On veut calculer RS.
Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
On connaît RT, le côté à l'angle 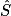 , et on veut calculer la longueur RS du côté .
, et on veut calculer la longueur RS du côté .
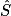 , et on veut calculer la longueur RS du côté .
, et on veut calculer la longueur RS du côté . On va donc utiliser de l'angle.
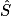 =
= 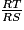 ; d'où RS = (arrondi à l'unité).
; d'où RS = (arrondi à l'unité).On connaît le côté opposé à l'angle 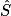 et on cherche le côté adjacent.
et on cherche le côté adjacent.
Il faut donc utiliser la tangente de l'angle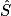 .
.
tan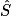 =
= 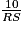 ; RS =
; RS = 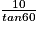
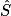 et on cherche le côté adjacent.
et on cherche le côté adjacent.Il faut donc utiliser la tangente de l'angle
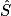 .
.tan
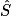 =
= 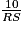 ; RS =
; RS =