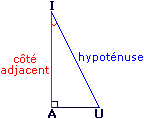
Cas d'un triangle AIU rectangle en A
 |
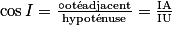
d'où IA = IU × cos Î ;
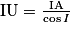
Dans AIU, on a aussi : 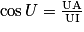
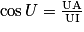
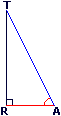
Cas d'un triangle RAT rectangle en R
Dans le triangle RAT, AR = 3 ; RT = 4 ; AT = 5.
 |
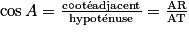
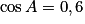
d'où
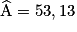 (valeur approchée).
(valeur approchée). Attention à bien repérer le côté adjacent à l'angle (celui qui est « à côté de » l'angle).
Exercice n°1
En utilisant la calculatrice, détermine la mesure en degré de l'angle 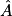 .
.
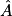 .
. Écrivez les réponses dans les zones colorées.
1. cos 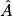 = 0,8
= 0,8
→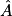
 ° à 0,1° près.
° à 0,1° près.
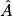 = 0,8
= 0,8→
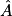
 ° à 0,1° près.
° à 0,1° près. 2. cos 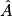 = 0,5
= 0,5
→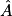
 ° à 0,1° près.
° à 0,1° près.
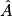 = 0,5
= 0,5→
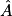
 ° à 0,1° près.
° à 0,1° près. 3. cos 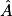 =
= 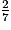
→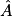
 ° à 0,1° près.
° à 0,1° près.
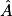 =
= 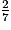
→
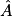
 ° à 0,1° près.
° à 0,1° près.Exercice n°2
Calcule l'angle 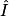 et la distance OC (arrondie au dixième).
et la distance OC (arrondie au dixième).
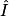 et la distance OC (arrondie au dixième).
et la distance OC (arrondie au dixième). Écrivez les réponses dans les zones colorées.
1.
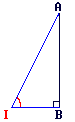 |
IA = 6
IB = 3
cos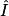 =
=
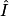 = °
= °
IB = 3
cos
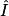 =
=  = °
= ° 2.
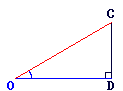 |
OD = 7
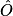 = 30°
= 30°
cos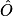 = 0,86
= 0,86
OC =
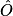 = 30°
= 30°cos
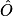 = 0,86
= 0,86OC =
1. cos 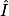 =
= 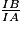 = 0,5.
= 0,5.
Les touches INV COS de la calculatrice donnent :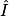 = 60°.
= 60°.
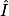 =
= 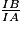 = 0,5.
= 0,5.Les touches INV COS de la calculatrice donnent :
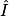 = 60°.
= 60°. 2. cos 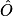 =
= 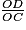 .
.
Donc 0,86 =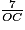 et OC = 7 ÷ 0,86.
et OC = 7 ÷ 0,86.
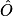 =
= 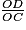 .
.Donc 0,86 =
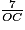 et OC = 7 ÷ 0,86.
et OC = 7 ÷ 0,86. Exercice n°3
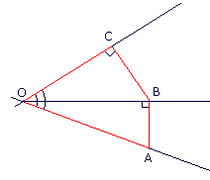 |
Sur la figure ci-contre, chaque angle marqué mesure 30° et OA = 12 cm.
On veut calculer le périmètre p du périmètre OABC.
On veut calculer le périmètre p du périmètre OABC.
Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
Dans le triangle OAB rectangle en B, on peut écrire :
- = OA × cos 30° = 12 × cos 30° (1)
- = OA × cos 60° = × cos 60° = × 0,5 = (2)
Dans le triangle OBC rectangle en C, on peut écrire :
- CO = × cos 30° (3)
- BC = × cos 60° (4)
- CO = × (cos 30°)2 (3)
- BC = × cos 60° (4)
p = OA + AB + BC + CO. En utilisant (1), (2), (3), (4), on obtient :
p = + × cos 30° + × (cos 30°)2
La calculatrice donne : p = 32,2 cm
p = + × cos 30° + × (cos 30°)2
La calculatrice donne : p = 32,2 cm
Exercice n°4
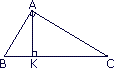 |
ABC est un triangle rectangle en A.
K est le pied de la perpendiculaire issue de A sur (BC).
On donne AB = 5 et BK = 3.
K est le pied de la perpendiculaire issue de A sur (BC).
On donne AB = 5 et BK = 3.
a. Coche la ou les bonne(s) réponse(s).
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
|
b. Calcule 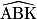 et
et 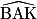
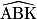 et
et 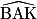
Écrivez les réponses dans les zones colorées.
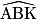
 ° à 0,1° près.
° à 0,1° près.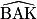
 ° à 0,1° près.
° à 0,1° près. a. Rappelle-toi que, dans le triangle IJK rectangle en J, cos 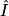 =
= 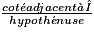
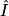 =
= 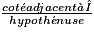
b. cos 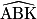 =
= 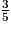 ; d'où
; d'où 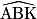 = 53,1°.
= 53,1°.
Dans un triangle rectangle, les deux angles aigus sont complémentaires.
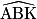 +
+ 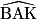 = 90°
= 90°
D'où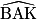 = 36,9°.
= 36,9°.
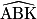 =
= 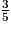 ; d'où
; d'où 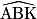 = 53,1°.
= 53,1°. Dans un triangle rectangle, les deux angles aigus sont complémentaires.
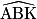 +
+ 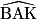 = 90°
= 90°D'où
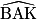 = 36,9°.
= 36,9°.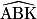 =
= 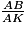
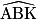 =
= 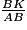
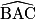 =
=