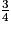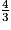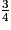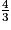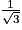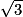Signaler une erreur
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques
Imprimer
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques
Le cosinus et le sinus
Dans un triangle ABC rectangle en A, on a :
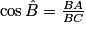
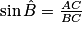
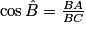
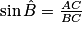
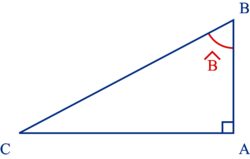 |
On retient :
cosinus d'un angle aigu =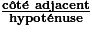
sinus d'un angle aigu =
cosinus d'un angle aigu =
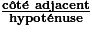
sinus d'un angle aigu =

La tangente
Dans un triangle ABC rectangle en A, on a :
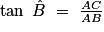 .
.
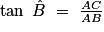 .
. |
On retient :
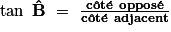
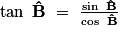
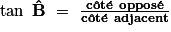
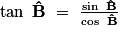
Exercice n°1
Vrai ou faux ?
1. 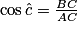
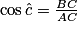
Cochez la bonne réponse.
| ||
|
2. 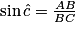
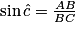
Cochez la bonne réponse.
| ||
|
3. 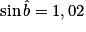
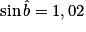
Cochez la bonne réponse.
| ||
|
1. 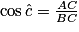 .
.
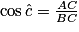 .
. 3. Le sinus d'un angle est toujours inférieur à 1.
Exercice n°2
Combien vaut la tangente des angles cités ci-dessous ?
Coche la bonne réponse.
Coche la bonne réponse.
a. Soit ABC un triangle rectangle en A avec AB = 6 et AC = 8.
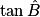 =
=
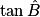 =
= Cochez la bonne réponse.
| ||
|
b. Dans le même triangle ABC, 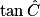 =
=
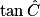 =
= Cochez la bonne réponse.
| ||
|
c. Le cosinus d'un angle 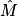 vaut
vaut 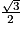 et son sinus
et son sinus 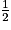 .
.
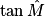 =
=
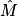 vaut
vaut 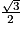 et son sinus
et son sinus 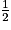 .
.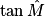 =
= Cochez la bonne réponse.
| ||
|
a et b. 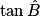 =
= 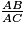
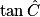 =
= 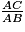
Pense à simplifier tes fractions.
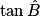 =
= 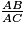
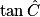 =
= 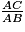
Pense à simplifier tes fractions.
c. 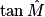 =
= 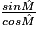 =
= 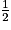 ×
×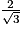
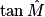 =
= 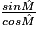 =
= 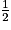 ×
×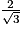
Signaler une erreur
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques
Imprimer
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques
Mathématiques - Réviser une notion
Énoncer les formules trigonométriques