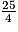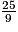Signaler une erreur
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès
Imprimer
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès
Exemple 1
• Les droites (EF) et (GH) sont parallèles.
Donc, d'après le théorème de Thalès appliqué aux triangles DEF et DGH, on a :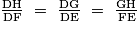
Donc, d'après le théorème de Thalès appliqué aux triangles DEF et DGH, on a :
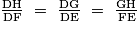
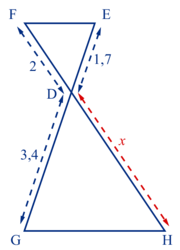 |
• On remplace les longueurs connues par leurs valeurs numériques et la valeur cherchée par l'inconnue x : 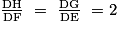 .
.
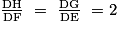 .
.• On obtient : x = 4.
Exemple 2
• De même, les droites (DE) et (BC) sont parallèles.
Donc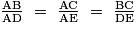 .
.
Donc
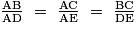 .
.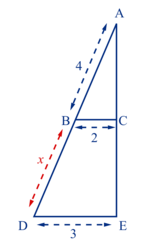 |
• On en déduit que : 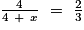 .
.
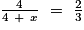 .
.• On obtient : x = 2.
Exercice n°1
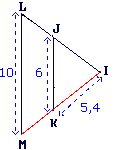 |
JKML est un trapèze.
JK = 6 ; IK = 5,4 et LM = 10.
Détermine les longueurs suivantes.
JK = 6 ; IK = 5,4 et LM = 10.
Détermine les longueurs suivantes.
Écrivez les réponses dans les zones colorées.
IM = 9 et KM = 3.6|3,6|3.60|3,60.
JKML est un trapèze donc (JK) // (LM) et les triangles IJK et ILM sont en situation de Thalès.
Alors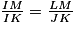 , soit
, soit 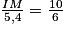
IM = (10 × 5,4) ÷ 6 = 9.
KM = IM − IK = 9 − 5,4.
Alors
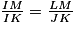 , soit
, soit 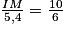
IM = (10 × 5,4) ÷ 6 = 9.
KM = IM − IK = 9 − 5,4.
Exercice n°2
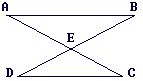 |
On donne : (AB) // (CD) ; AB = 5 ; CD = 4 ; BD = 5.
Que vaut BE ?
Que vaut BE ?
Coche la bonne réponse.
Cochez la bonne réponse.
| ||
| ||
|
Appliquons le théorème de Thalès :
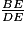 =
= 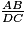
Appelons x, la longueur BE ; DE = 5 − x.
On obtient l'équation suivante :
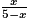 =
= 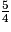
4x = 5 (5 − x)
4x = 25 − 5x
9x = 25
x =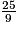
BE =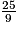
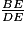 =
= 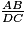
Appelons x, la longueur BE ; DE = 5 − x.
On obtient l'équation suivante :
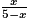 =
= 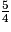
4x = 5 (5 − x)
4x = 25 − 5x
9x = 25
x =
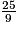
BE =
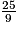
Signaler une erreur
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès
Imprimer
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès
Mathématiques - Réviser une notion
Calculer une longueur au moyen du théorême de Thalès