Signaler une erreur
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès
Imprimer
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès
Le théorème de Thalès
Quand on coupe deux droites sécantes au point A par deux droites parallèles (MN) et (BC), on obtient deux triangles ABC et AMN.
Le théorème de Thalès énonce que, dans ce type de configuration, les longueurs des côtés d'un triangle sont proportionnels aux côtés associés de l'autre triangle.
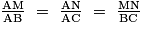
Le théorème de Thalès énonce que, dans ce type de configuration, les longueurs des côtés d'un triangle sont proportionnels aux côtés associés de l'autre triangle.
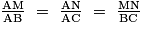
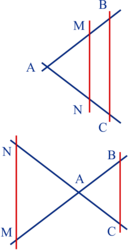 |
Remarques
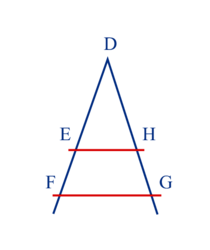
On ne peut pas appliquer le théorème de Thalès si la figure ne comporte pas de droites parallèles.
Ici : (EH) // (FG).
Quand on écrit l'égalité des trois quotients, on met :
Ici : (EH) // (FG).
Quand on écrit l'égalité des trois quotients, on met :
- au numérateur, un côté du premier triangle ;
- au dénominateur, le côté associé du second triangle.
Ici :  .
.
 .
. |
Exercice n°1
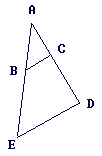 |
On donne : AB = 4 ; AE = 10 ; (BC) // (DE).
Complète avec un nombre en écriture décimale.
Complète avec un nombre en écriture décimale.
Écrivez les réponses dans les zones colorées.
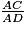 = 0.4|0,4|0.40|0,40.
= 0.4|0,4|0.40|0,40.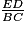 = 2.5|2,5|2.50|2,50.
= 2.5|2,5|2.50|2,50.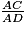 =
= 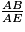 =
= 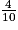 = 0,4.
= 0,4.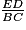 =
= 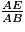 =
= 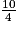 = 2,5.
= 2,5.
Signaler une erreur
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès
Imprimer
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès
Mathématiques - Réviser une notion
Appliquer le théorème de Thalès

