À l'aide de la propriété de Thalès, on calcule une longueur, lorsque l'on connaît les trois autres longueurs.
Exemple 1
 |
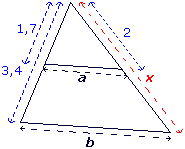On peut écrire :
.
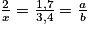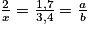.a et b étant inconnus, on utilise :
.
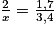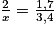.On obtient :
x = 4.
x = 4.
Exemple 2
 |
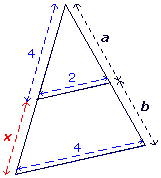On peut écrire :
.
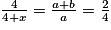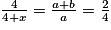.a et b étant inconnus, on utilise :
.
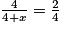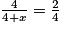.On obtient :
x = 4.
x = 4.
Exercice n°1
 |
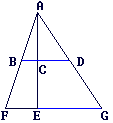On donne : (BD) // (FG)
CD = 4
CB = 2
EG = 8
CD = 4
CB = 2
EG = 8
Calcule le rapport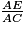 
et déduis-en la valeur de EF.
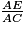et déduis-en la valeur de EF. Écrivez les réponses dans les zones colorées.
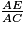= et EF = . Applique la propriété de Thalès dans le triangle AEG puis dans le triangle AEF.
• Les côtés de ACD et AEG sont proportionnels.
Donc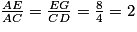
.
Donc
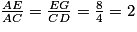.• Les côtés de ABC et AFE sont proportionnels.
Donc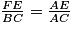
.
Or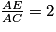
.
Donc EF = 2 × BC = 4.
Donc
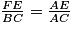.Or
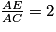.Donc EF = 2 × BC = 4.
Exercice n°2
 |
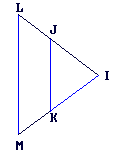JKML est un trapèze.
JK = 6 ; IK = 5,4 et LM = 10.
JK = 6 ; IK = 5,4 et LM = 10.
Calcule les longueurs des côtés [IM] et [KM].
Écrivez les réponses dans les zones colorées.
IM = et KM = .
JKML est un trapèze donc (JK) // (/LM) et les côtés des triangles IJK et ILM sont proportionnels.
Alors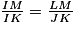
, soit 
.
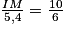IM = (10 × 5,4) ÷ 6 = 9.
KM = IM − IK = 9 − 5,4.
Alors
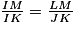, soit 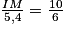.IM = (10 × 5,4) ÷ 6 = 9.
KM = IM − IK = 9 − 5,4.
Exercice n°3
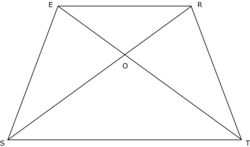
TRES est un trapèze de bases [RE] et [ST]. Ses diagonales sont sécantes en O. Parmi ces propositions, lesquelles sont exactes ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
= 
= 
= 
= 
Trace le trapèze TRES et repère les droites parallèles.
• Les côtés des triangles ORE et SOT sont proportionnels. On obtient :
= 
= 
.
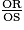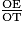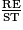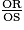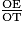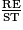= = .• On obtient aussi OR × OT = OS × OE, d'où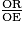 
= 
.
= . |
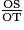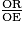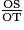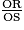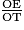
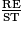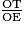
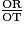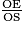
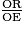