Définition
• Soit a, un nombre positif. 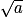 est le nombre positif qui, élevé au carré, donne a.
est le nombre positif qui, élevé au carré, donne a.
Ainsi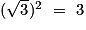
On a aussi :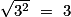 donc
donc 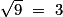 .
.
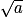 est le nombre positif qui, élevé au carré, donne a.
est le nombre positif qui, élevé au carré, donne a.Ainsi
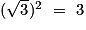
On a aussi :
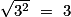 donc
donc 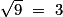 .
.• Remarques :
On ne peut calculer la racine carrée que d'un nombre positif.
Une racine carrée est toujours égale à un nombre positif :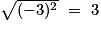 .
.
On ne peut calculer la racine carrée que d'un nombre positif.
Une racine carrée est toujours égale à un nombre positif :
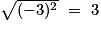 .
.Utilisation de la touche 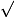 de la calculatrice
de la calculatrice
• On veut calculer 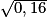 .
.
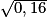 .
.La calculatrice affiche 0,4. Donc : 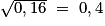 .
.
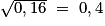 .
.• On veut calculer 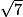 .
.
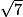 .
.La calculatrice affiche 2,6457513 qui est une valeur approchée de 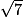 .
.
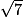 .
.Exercice n°1
Vrai ou faux ?
1. On ne peut calculer la racine carrée que d'un nombre positif.
Cochez la bonne réponse.
| ||
|
2. La racine carrée d'un nombre peut être égale à -1.
Cochez la bonne réponse.
| ||
|
3. La calculatrice permet de trouver la valeur exacte de 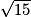 .
.
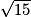 .
. Cochez la bonne réponse.
| ||
|
1. Une racine carrée est toujours égale à un nombre positif.
2. 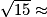 3,782.
3,782.
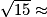 3,782.
3,782.Exercice n°2
Complète les égalités en t'aidant de la calculatrice pour les deux dernières. Pour les nombres irrationnels, donne une valeur arrondie à 0,01 près.
Écrivez les réponses dans les zones colorées.
1. 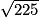 =
=
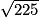 =
= 2. 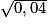 =
=
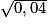 =
= 3. 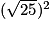 =
=
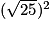 =
= 4. 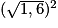 =
=
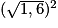 =
= 5. 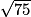 =
=
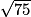 =
= 6. 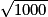 =
=
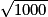 =
= Pour donner une valeur approchée à 0,01 près, il faut garder deux décimales.
5. 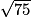 = 8,66025…
= 8,66025…
La valeur approchée à 0,01 près est donc 8,66.
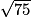 = 8,66025…
= 8,66025…La valeur approchée à 0,01 près est donc 8,66.
6. 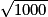 = 31,6227…
= 31,6227…
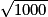 = 31,6227…
= 31,6227…Exercice n°3
Complète l'égalité quand c'est possible.
Si l'expression n'a pas de sens, choisis « pas de sens ».
Si l'expression n'a pas de sens, choisis « pas de sens ».
Faites glisser les étiquettes dans les zones prévues à cet effet.
« pas de sens »
-3
3
a. (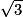 )2 =
)2 =
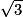 )2 =
)2 = imcAnswer7|imcAnswer12?
b. −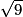 =
=
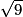 =
= imcAnswer8|imcAnswer11?
c. 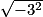 =
=
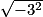 =
= imcAnswer9|imcAnswer10?
d. 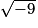 =
=
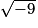 =
= imcAnswer9|imcAnswer10?
e. −(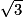 )2 =
)2 =
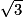 )2 =
)2 = imcAnswer8|imcAnswer11?
f. 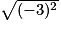 =
=
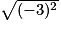 =
= imcAnswer7|imcAnswer12?
c. Le signe « − » n'est pas concerné par le carré.
d. Le nombre sous le radical est −9, or un nombre négatif ne peut pas être un carré.
f. Le nombre sous le radical est 9.
Exercice n°4
Quelles sont les égalités justes ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
|
• 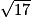
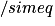 4,123
4,123
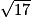
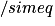 4,123
4,123• 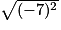 = −7
= −7
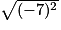 = −7
= −7• 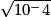 = −10−2
= −10−2
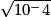 = −10−2
= −10−2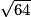 = 8
= 8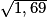 = 1,3
= 1,3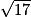 = 4,12
= 4,12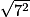 = 7
= 7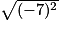 = −7
= −7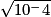 = −102
= −102 
