Signaler une erreur
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes
Imprimer
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes
Énoncé
• Une urne contient 6 boules de couleur rouge, 4 de couleur noire et 3 boules de couleur bleue.
Une seconde urne contient 2 de couleur verte et 5 de couleur jaune.
On ne peut pas différencier les boules.
Une seconde urne contient 2 de couleur verte et 5 de couleur jaune.
On ne peut pas différencier les boules.
• On tire une boule dans la première urne puis une boule dans la seconde urne, le tirage dans la seconde urne est indépendant du tirage réalisé dans la première.
On note :
On note :
- R l'événement « obtenir une boule rouge » ;
- N l'événement « obtenir une boule noire » ;
- B l'événement « obtenir une boule bleue » ;
- V l'événement « obtenir une boule verte » ;
- J l'événement « obtenir une boule jaune ».
Calcul des probabilités
• Les calculs de probabilité dans la première urne donnent :
- p(R) = \frac{6}{13} ;
- p(N) = \frac{4}{13} ;
- p(B) = \frac{3}{13}.
• Les calculs de probabilité dans la seconde urne donnent :
- p(V) = \frac{2}{7} ;
- p(J) = \frac{5}{7}.
• Voici l'arbre pondéré décrivant la situation :
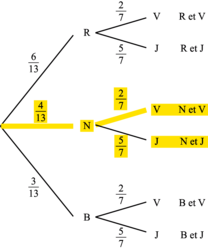 |
Au bout de chaque branche, on trouve l'événement associé au tirage des deux urnes.
On a ainsi toutes les possibilités : une boule rouge et une boule verte, une boule rouge et une boule jaune, etc.
On a ainsi toutes les possibilités : une boule rouge et une boule verte, une boule rouge et une boule jaune, etc.
• Pour calculer la probabilité de l'événement « obtenir une boule noire et une boule verte », on peut se « promener » dans l'arbre. On obtient : \frac{4}{13} × \frac{2}{7} = \frac{8}{91}.
• On applique la règle suivante :
Dans un arbre, la probabilité de l'issue auquel conduit un chemin est égale au produit des probabilités rencontrées le long du chemin.
Dans un arbre, la probabilité de l'issue auquel conduit un chemin est égale au produit des probabilités rencontrées le long du chemin.
Signaler une erreur
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes
Imprimer
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes
Mathématiques - Réviser une notion
Réaliser une expérience à deux étapes

