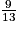On peut visualiser toutes les issues possibles d'une expérience aléatoire à l'aide d'un arbre, appelé arbre des possibles.
Exemples
• On lance une pièce de monnaie et on regarde la face supérieure.
Les issues possibles de cette expérience aléatoire sont : pile, face.
On peut construire un arbre pour visualiser les issues :
Les issues possibles de cette expérience aléatoire sont : pile, face.
On peut construire un arbre pour visualiser les issues :
 |
• Dans une roue équilibrée, la partie verte occupe la moitié du disque et les parties bleue, rouge et beige occupent respectivement 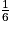 .
.
Les issues possibles sont V : verte ; Bl : bleue ; Be : beige et R : rouge.
L'arbre des possibles est donc :
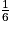 .
.Les issues possibles sont V : verte ; Bl : bleue ; Be : beige et R : rouge.
L'arbre des possibles est donc :
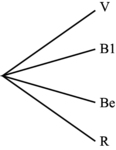 |
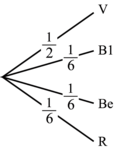
• On peut indiquer sur chaque branche de l'arbre les probabilités des événements, l'arbre est alors un arbre pondéré.
Par exemple, pour la roue, on a :
Par exemple, pour la roue, on a :
 |
Remarque : la somme des probabilités est égale à 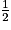 +
+ 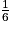 +
+ 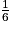 +
+ 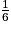 =
= 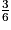 +
+ 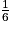 +
+ 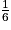 +
+ 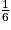 = 1.
= 1.
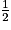 +
+ 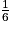 +
+ 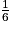 +
+ 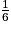 =
= 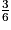 +
+ 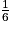 +
+ 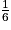 +
+ 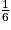 = 1.
= 1.• En utilisant la roue précédente, on considère l'événement R : « obtenir la couleur rouge ».
L'événement contraire noté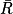 est : « ne pas obtenir la couleur rouge ».
est : « ne pas obtenir la couleur rouge ».
On veut calculer la probabilité de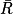 . On a deux méthodes :
. On a deux méthodes :
1. En utilisant l'arbre pondéré, on additionne toutes les probabilités, sauf la probabilité de l'événement R :
p(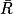 ) =
) = 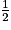 +
+ 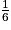 +
+ 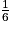 +
+ 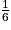 =
= 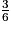 +
+ 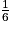 +
+ 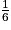 =
= 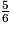 .
.
2. On sait que p(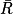 ) = 16 et p(
) = 16 et p(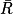 ) + p(
) + p(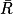 ) = 1
) = 1
Donc p(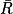 ) = 1 −
) = 1 − 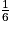 =
= 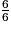 −
− 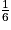 =
= 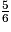 .
.
L'événement contraire noté
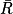 est : « ne pas obtenir la couleur rouge ».
est : « ne pas obtenir la couleur rouge ».On veut calculer la probabilité de
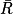 . On a deux méthodes :
. On a deux méthodes :1. En utilisant l'arbre pondéré, on additionne toutes les probabilités, sauf la probabilité de l'événement R :
p(
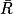 ) =
) = 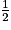 +
+ 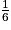 +
+ 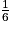 +
+ 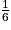 =
= 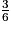 +
+ 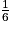 +
+ 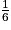 =
= 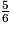 .
.2. On sait que p(
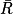 ) = 16 et p(
) = 16 et p(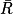 ) + p(
) + p(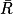 ) = 1
) = 1Donc p(
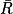 ) = 1 −
) = 1 − 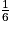 =
= 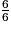 −
− 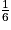 =
= 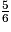 .
.Exercice n°1
Une urne contient 6 boules de couleur rouge, 4 de couleur noire et 3 boules de couleur bleue indiscernables au toucher.
On veut construire un arbre pondéré pour représenter la situation.
On veut construire un arbre pondéré pour représenter la situation.
1. Combien l'arbre doit-il avoir de branches ?
Cochez la bonne réponse.
| ||
| ||
|
2. Quelle est la probabilité de tirer une boule rouge ?
Écrivez les réponses dans les zones colorées.
→ /
3. Quelle est la probabilité de tirer une boule noire ?
Écrivez les réponses dans les zones colorées.
→ /
4. Quelle est la probabilité de tirer une boule bleue ?
Écrivez les réponses dans les zones colorées.
→ /
5. Quel arbre pondéré représente la situation décrite précédemment ?
 |
Cochez la bonne réponse.
| ||
|
6. Quelle est la probabilité de ne pas tirer une boule noire ?
Écrivez les réponses dans les zones colorées.
→ /
1. Il y a trois couleurs différentes.
2. Il ya 6 boules rouges dans l'urne qui en contient 13.
3. Il y a 4 boules noires dans l'urne qui en contient 13.
4. Il y a 3 boules bleues dans l'urne qui en contient 13.
5. Sur les branches d'un arbre pondéré, on doit avoir les probabilités et non les nombres d'issues.
6. En utilisant l'arbre de la question précédente, on additionne les probabilités des événements « tirer une boule rouge », « tirer une boule bleue » :
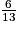 +
+ 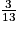 =
= 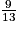
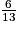 +
+ 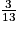 =
=