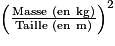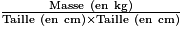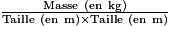Un algorithme est la décomposition d'une action en instructions élémentaires.
Les calculs nécessaires à la résolution d'un problème, les consignes pour un tracé géométrique, les étapes pour trier des données constituent des algorithmes.
L'énoncé en français doit être traduit en langage machine pour effectuer un traitement sur calculatrice ou ordinateur.
Les calculs nécessaires à la résolution d'un problème, les consignes pour un tracé géométrique, les étapes pour trier des données constituent des algorithmes.
L'énoncé en français doit être traduit en langage machine pour effectuer un traitement sur calculatrice ou ordinateur.
Instructions d'un algorithme élémentaire
Un algorithme comporte en principe quatre étapes.
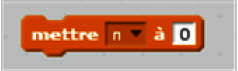
- Indication des variables : une variable sert à stocker une valeur numérique ou un mot. Il faut déclarer les données de l'énoncé et désigner les variables qui permettront de stocker les résultats intermédiaires lors du traitement des instructions. Lorsqu'il s'agit d'un tracé, il n'y a pas de variables ;
- Début : on affecte les données dans des variables, on place le curseur sur l'écran, on choisit une taille pour le stylo, on choisit une orientation pour le prochain tracé ;
 |
Exemple 2 (dans Scratch) : on place le curseur et on définit une orientation.
 |
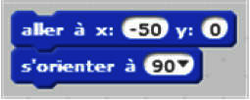- Traitement : on note l'ensemble des instructions de calcul, les boucles de répétition, les tests à effectuer, les déplacements sur l'écran à effectuer ;
 |
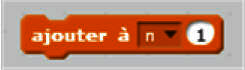Exemple 2 (dans Scratch) : on définit un déplacement, après avoir défini une orientation.
 |
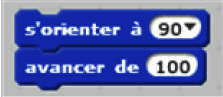- Sortie : lorsque toutes les opérations sont exécutées il faut communiquer les résultats, c'est-à-dire les écrire ou, lorsqu'il s'agit d'une figure, la tracer.
Condition dans un algorithme élémentaire
Une action est effectuée si la condition est vérifiée. Si elle n'est pas vérifiée, une autre action est effectuée ou, si rien n'est précisé, le programme passe à l'étape suivante.
Si condition, alors traitement 1.
Sinon traitement 2.
FinSi
Sinon traitement 2.
FinSi
Exemple (dans Scratch) :
 |
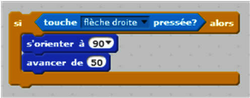Si la touche flèche droite est pressée, le curseur avance de 50 à l'horizontale vers la droite. Si ce n'est pas le cas, ici, il n'y a pas de « traitement 2 ».
Boucles dans un algorithme élémentaire
Dans un algorithme, la répétition de la même suite d'instructions un certain nombre de fois s'appelle une « boucle ».
La question importante est « comment arrêter la boucle » ?
Il y a deux méthodes à choisir en fonction du problème : soit on connaît le nombre de fois que l'on doit effectuer la répétition, soit on connaît un test d'arrêt.
La question importante est « comment arrêter la boucle » ?
Il y a deux méthodes à choisir en fonction du problème : soit on connaît le nombre de fois que l'on doit effectuer la répétition, soit on connaît un test d'arrêt.
Il y a trois structures possibles.
- Avec un compteur : pour variable variant de …, faire traitement. FinPour
 |
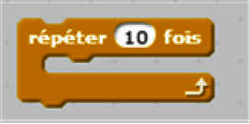- Avec une condition : tant que condition, faire traitement. FinTantque
- Avec répétition jusqu'à condition : répète traitement jusqu'à condition. FinTantque
 |
 |
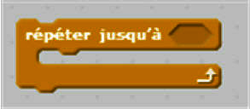Exercice n°1
On donne le programme de calcul suivant :
 |
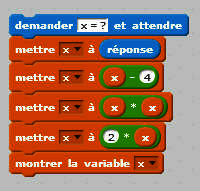Pour une valeur x donnée, que calcule-t-il ?
Cochez la bonne réponse.
| ||
| ||
|
Dans un premier temps, le programme associe à la valeur x rentrée, la valeur x − 4.
Dans un deuxième temps, il associe à la valeur x le carré de la valeur précédente, qui est (x − 4)2.
Dans un troisième temps, il associe à la valeur x le double de la valeur précédente, qui est 2×(x − 4)2.
Finalement, le programme associe à la valeur x rentrée la valeur 2(x − 4)2.
Dans un deuxième temps, il associe à la valeur x le carré de la valeur précédente, qui est (x − 4)2.
Dans un troisième temps, il associe à la valeur x le double de la valeur précédente, qui est 2×(x − 4)2.
Finalement, le programme associe à la valeur x rentrée la valeur 2(x − 4)2.
Exercice n°2
On donne le programme de calcul suivant :
|
Que retourne le programme lorsque l'on rentre la valeur x = 3 ?
Écrivez la réponse dans la zone colorée.
Lorsque l'on rentre la valeur x = 3, le programme retourne la valeur .
À la valeur x rentrée, le programme associe la valeur 2(x − 4)2.
Lorsque l'on rentre la valeur x = 3, le programme retourne donc la valeur 2×(3 − 4)2 = 2×(−1)2 = 2×1 = 2.
Lorsque l'on rentre la valeur x = 3, le programme retourne donc la valeur 2×(3 − 4)2 = 2×(−1)2 = 2×1 = 2.
Exercice n°3
Un programme Scratch permet aux élèves d'analyser la valeur de leur indice de masse corporelle (IMC) en cours de SVT.
 |
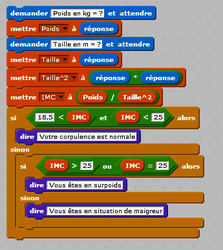En observant le programme, laquelle de ces formules donne la valeur de l'IMC ?
Cochez la bonne réponse.
| ||
| ||
|
Le programme demande tout d'abord le poids (en kg) de l'élève.
Le programme demande ensuite la taille de l'élève (en m), puis calcule cette valeur au carré en utilisant la variable «~Taille^2~».
Dans la variable « IMC », il y a donc le résultat du calcul :
.
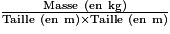Le programme demande ensuite la taille de l'élève (en m), puis calcule cette valeur au carré en utilisant la variable «~Taille^2~».
Dans la variable « IMC », il y a donc le résultat du calcul :
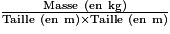. Exercice n°4
Un programme Scratch permet aux élèves d'analyser la valeur de leur indice de masse corporelle (IMC) en cours de SVT.
|
Pour un élève qui mesure 178 cm et pèse 70 kg, que retourne le programme ?
Cochez la bonne réponse.
| ||
| ||
|
Si un élève mesure 178 cm = 1,78 m et pèse 70 kg, son IMC est de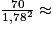 
22,1 au dixième près.
Le programme retourne donc « Votre corpulence est normale ».
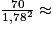22,1 au dixième près.Le programme retourne donc « Votre corpulence est normale ».
