Règle
Un produit de facteur est nul lorsque l'un des facteurs est nul.(ax + b) (cx + d) est le produit du facteur (ax + b) par le facteur (cx + d).
Ce produit est donc nul lorsque ax + b = 0 ou cx + d = 0.
Exemples
• Résoudre l'équation (E) : 3x(2x + 6) = 0.
3x(2x + 6) est un produit de facteurs : les facteurs sont 3x et (2x + 6).
Donc 3x(2x + 6) = 0 lorsque 3x = 0 ou 2x + 6 = 0.
C'est-à-dire x = 0 ou x = -3.
L'équation (E) admet deux solutions : 0 et -3.
3x(2x + 6) est un produit de facteurs : les facteurs sont 3x et (2x + 6).
Donc 3x(2x + 6) = 0 lorsque 3x = 0 ou 2x + 6 = 0.
C'est-à-dire x = 0 ou x = -3.
L'équation (E) admet deux solutions : 0 et -3.
• Attention, il faut parfois commencer par factoriser.
Ainsi, l'équation 9x2 − 16 = 0 peut s'écrire : (3x − 4)(3x + 4) = 0.
(3x − 4)(3x + 4) est un produit de facteurs : les facteurs sont (3x − 4) et (3x + 4).
Donc 9x2 − 16 = 0 lorsque 3x − 4 = 0 ou 3x + 4 = 0.
C'est-à-dire x =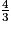
ou x = 
.
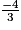L'équation 9x2 − 16 = 0 admet deux solutions :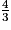
et 
.
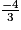Ainsi, l'équation 9x2 − 16 = 0 peut s'écrire : (3x − 4)(3x + 4) = 0.
(3x − 4)(3x + 4) est un produit de facteurs : les facteurs sont (3x − 4) et (3x + 4).
Donc 9x2 − 16 = 0 lorsque 3x − 4 = 0 ou 3x + 4 = 0.
C'est-à-dire x =
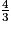ou x = 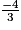.L'équation 9x2 − 16 = 0 admet deux solutions :
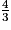et 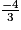.Exercice n°1
Pour résoudre une équation du type (ax + b) (cx + d) = 0, on résout les équations ax + b = 0 et cx + d = 0.
Cochez la bonne réponse.
| ||
|
Pour résoudre l'équation (2x + 1)2 − (x + 3) (2x + 1) = 0, on factorise (2x + 1) dans le membre de gauche.
Cochez la bonne réponse.
| ||
|
Exercice n°2
Résous les équations suivantes.
Écrivez les réponses dans les zones colorées.
1. (3x − 12) (x + 3) = 0
Solutions (dans l'ordre croissant) : et .
Solutions (dans l'ordre croissant) : et .
2. (x − 1) (-x − 2) = 0
Solutions (dans l'ordre croissant) : et .
Solutions (dans l'ordre croissant) : et .
3. (x + 3) (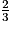
x + 2) = 0
Solution : .
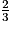x + 2) = 0Solution : .
3. (x + 3) (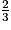
x + 2) = 0 signifie que : x + 3 = 0.
Donc x = -3.
Ou
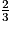x + 2 = 0 donc x = -2x
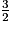, soit x = -3.
-3 est une solution double.
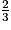x + 2) = 0 signifie que : x + 3 = 0.Donc x = -3.
Ou
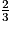x + 2 = 0 donc x = -2x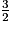, soit x = -3.-3 est une solution double.
Exercice n°3
Résous les équations suivantes.
Écrivez les réponses dans les zones colorées.
a. (2x + 4)(3x)(x − 5) = 0
Solutions (dans l'ordre croissant) : −2 ; et .
Solutions (dans l'ordre croissant) : −2 ; et .
b. (2x + 8)(x2 −1 ) = 0
Solutions (dans l'ordre croissant) : ; et .
Solutions (dans l'ordre croissant) : ; et .
b. (2x + 8)(x2 − 1) = 0 s'écrit aussi :
(2x + 8)(x + 1)(x − 1) = 0
Cela signifie que :
2x + 8 = 0 donc x = −4
ou x + 1 = 0 donc x = −1
ou x − 1 = 0 donc x = 1.
(2x + 8)(x + 1)(x − 1) = 0
Cela signifie que :
2x + 8 = 0 donc x = −4
ou x + 1 = 0 donc x = −1
ou x − 1 = 0 donc x = 1.
Exercice n°4
Résous les équations suivantes.
Écrivez les réponses dans les zones colorées.
100x2 − 200x + 100 = 0
L'ensemble des solutions de cette équation est :
S = {}.
L'ensemble des solutions de cette équation est :
S = {}.
64x2 + 128x + 64 = 0
L'ensemble des solutions de cette équation est :
S = {}.
L'ensemble des solutions de cette équation est :
S = {}.
81x2 − 81 = 0
L'ensemble des solutions de cette équation est :
S = { ; }.
L'ensemble des solutions de cette équation est :
S = { ; }.
• On reconnaît (a − b)2.
• On reconnaît (a + b)2.
• On reconnaît a2 − b2.
