Pour obtenir une équation du type : (ax + b)(cx + d) = 0, on doit :
- passer tous les termes non nuls à gauche du signe égal ;
- factoriser le membre de gauche.
Exemple 1
(E) : 81x2 – (x + 2)2 = 0
• On reconnaît dans le membre de gauche la différence de deux carrés.
On factorise donc en utilisant :
a2 – b2 = (a + b)(a – b).
a2 – b2 = (a + b)(a – b).
(E) : (9x + x + 2)(9x – x – 2) = 0
• On est ramené à une équation produit que l'on sait résoudre.
(E) admet deux solutions :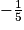 et
et 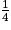 .
.
(E) admet deux solutions :
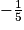 et
et 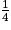 .
.Exemple 2
(E) : x2 – 9 = 2(x + 3)2
• On passe à gauche du signe égal tous les termes non nuls.
(E) : x2 – 9 – 2(x + 3)2 = 0
(E) : x2 – 9 – 2(x + 3)2 = 0
• On factorise la différence de deux carrés x2 – 9 ; on met ainsi en évidence le facteur commun (x + 3).
(E) : (x – 3)(x + 3) – 2(x + 3)2 = 0
(E) : (x + 3) [x – 3 – 2(x + 3)] = 0
(E) admet deux solutions : –3 et –9.
Exercice n°1
Soit l'équation (E) : (3x + 1)2 = (x + 3)2.
Résous-la en utilisant la méthode proposée.
Résous-la en utilisant la méthode proposée.
Écrivez les réponses dans les zones colorées.
1. On rend le membre de droite égal à zéro et on factorise le membre de gauche. (E) devient :
(x + ) (x − ) = 0.
(x + ) (x − ) = 0.
2. (E) admet donc deux solutions :
et (dans l'ordre croissant).
et (dans l'ordre croissant).
(3x + 1)2 − (x + 3)2 = 0
Rappelle-toi que :
a2 − b2 = (a + b) (a − b).
a2 − b2 = (a + b) (a − b).
Applique cette relation à (E) avec :
a + b = (3x + 1) + (x + 3)
a + b = 4x + 4
a + b = (3x + 1) + (x + 3)
a + b = 4x + 4
a − b = (3x + 1) − (x + 3)
a − b = 2x − 2.
a − b = 2x − 2.
Exercice n°2
Soit l'équation (E) : x2 − 4 = 3x − 6.
Résous-la en utilisant la méthode proposée.
Résous-la en utilisant la méthode proposée.
Écrivez les réponses dans les zones colorées.
1. On rend le membre de droite égal à zéro. Dans le membre de gauche, on met alors en facteur :
(x ).
(x ).
2. (E) admet donc deux solutions :
et (dans l'ordre décroissant).
et (dans l'ordre décroissant).
• Pense que :
x2 − 4 = (x − 2) (x + 2)
3x − 6 = 3 (x − 2).
x2 − 4 = (x − 2) (x + 2)
3x − 6 = 3 (x − 2).
• L'équation (E) s'écrit :
(x − 2) (x + 2) − 3 (x − 2) = 0
(x − 2) [(x + 2) − 3] = 0
(x − 2) (x − 1) = 0
(x − 2) (x + 2) − 3 (x − 2) = 0
(x − 2) [(x + 2) − 3] = 0
(x − 2) (x − 1) = 0

