Trois cousins, Zoé, Luc et Serge ont à eux trois 60 ans.
Quel est l'âge de chacun, sachant que Luc a le triple de l'âge de Zoé et que Serge a dix ans de moins que Luc ?
Choix de l'inconnue
Appelons x l'âge de Zoé.
On peut exprimer les âges des deux autres cousins en fonction de x.
- Luc a le triple de l'âge de Zoé, donc l'âge de Luc est 3x.
- Serge a dix ans de moins que Luc, donc l'âge de Serge est (3x − 10).
Mise en équation
On sait par ailleurs que la somme des âges des 3 cousins est de 60 ans.
Donc : x + 3x + (3x − 10) = 60.
Résolution de l'équation
| x + 3x + 3x − 10 | = 60 |
| 7x − 10 | = 60 |
| 7x | = 70 |
| x | = 10 |
Réponse à la question
Zoé a 10 ans ;Luc a 3 × 10 ans, soit 30 ans
et Serge a (30 − 10) ans, soit 20 ans.
Exercice n°1
On veut trouver trois nombres entiers consécutifs dont la somme est 135.
Écris l'équation qui te permet de répondre au problème, puis résous-là.
Écris l'équation qui te permet de répondre au problème, puis résous-là.
Écrivez les réponses dans les zones colorées.
1. Soit x le plus petit de ces entiers, l'équation correspondant à l'énoncé est la suivante :
+ ( + 1) + ( + ) = .
+ ( + 1) + ( + ) = .
2. Déduis-en la valeur…
- du plus petit nombre : ;
- des deux autres (dans l'ordre croissant) : ; .
1. Les nombres consécutifs sont x, x + 1 et x + 2.
x + x + 1 + x + 2 = 135
3x + 3 = 135
3x = 132
x = 44
x + x + 1 + x + 2 = 135
3x + 3 = 135
3x = 132
x = 44
2. Les nombres cherchés sont donc 44, 45 et 46.
Exercice n°2
Pauline a payé un cédérom 29 € avec 13 pièces, les unes de 1 €, les autres de 5 €.
Combien avait-elle de pièces de 1 € et de pièces de 5 € ? Complète le raisonnement.
Combien avait-elle de pièces de 1 € et de pièces de 5 € ? Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
1. Si on appelle x le nombre de pièces de 1 €, alors le nombre de pièces de 5 € est la différence :
( − ).
( − ).
2. L'équation correspondant à l'énoncé est :
+ ( − ) =
D'où 4x = et x = .
+ ( − ) =
D'où 4x = et x = .
3. Pauline avait donc pièces de 1 € et pièces de 5 €.
2. x fois la pièce de 1 € et (13 − x) fois la pièce de 5 € font la somme de 29 €.
L'équation du problème est donc : x + 5(13 − x) = 29.
On trouve que : x = 9.
L'équation du problème est donc : x + 5(13 − x) = 29.
On trouve que : x = 9.
3. On effectue ensuite 13 − 9 pour trouver le nombre de pièces de 5 €.
Exercice n°3
Complète les réponses suivantes.
Écrivez les réponses dans les zones colorées.
1. Un rectangle dont la longueur mesure 4 cm de plus que sa largeur a pour périmètre 20 cm. Quelles sont ses dimensions ?
Si x est la largeur, l'équation s'écrit :
= 2( + 4 + ).
Sa longueur est donc cm et sa largeur cm.
Si x est la largeur, l'équation s'écrit :
= 2( + 4 + ).
Sa longueur est donc cm et sa largeur cm.
2. Plusieurs enfants se groupent pour faire un cadeau à un ami. Si chacun verse 18 €, il manque 8 €. Si chacun verse 20 €, il reste 10 €. Combien de personnes participent au cadeau ?
Si x est le nombre de personnes, l'équation s'écrit :
x + = x − .
Il y a donc personnes.
Si x est le nombre de personnes, l'équation s'écrit :
x + = x − .
Il y a donc personnes.
1. 20 = 2(x + 4 + x), d'où x = 3.
Tu en déduis que la largeur du rectangle est 3 cm et que sa longueur est 7 cm (3 + 4).
Tu en déduis que la largeur du rectangle est 3 cm et que sa longueur est 7 cm (3 + 4).
2. 18x + 8 = 20x − 10
2x = 18
x = 9
2x = 18
x = 9
Exercice n°4
Jean a payé un discman 73 € avec 26 pièces, les unes de 2 €, les autres de 5 €.
Combien avait-il de pièces de 2 € et de pièces de 5 € ?
Combien avait-il de pièces de 2 € et de pièces de 5 € ?
Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
On appelle x le nombre de pièces de 2 € : x + ( − x) = d'où x = .
Jean avait donc pièces de 2 € et pièces de 5 €.
x fois la pièce de 2 € et (26 − x) fois la pièce de 5 € font la somme de 73 €.
L'équation du problème est donc : 2x + 5(26 − x) = 73.
On trouve que x = 19.
L'équation du problème est donc : 2x + 5(26 − x) = 73.
On trouve que x = 19.
On effectue ensuite 26 − 19 pour trouver le nombre de pièces de 5 €.
Exercice n°5
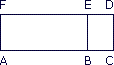 |
Sur la figure ci-contre, ABEF et BCDE sont des rectangles. On donne AC = 4 et CD = 1,3.
Quelle doit être la mesure de BC pour que le périmètre du rectangle BCDE soit la moitié de celui du rectangle ABEF ?
On pose BC = x. Complète en utilisant le signe / pour la barre de fraction.
On pose BC = x. Complète en utilisant le signe / pour la barre de fraction.
Écrivez les réponses dans les zones colorées.
L'équation qui traduit le problème est : (x + ) = [2( − x + )].
On a donc BC = .
• En fonction de x :
- le demi-périmètre du rectangle BCDE s'écrit (x + 1,3) ;
- son périmètre 2(x + 1,3) ;
- la longueur du rectangle ABEF (4 − x) ;
- son périmètre 2[(4 − x) + 1,3].
Or périmètre BCDE = 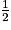 périmètre ABEF.
périmètre ABEF.
Donc 2(x + 1,3) =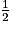 [2(4 − x + 1,3)].
[2(4 − x + 1,3)].
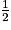 périmètre ABEF.
périmètre ABEF.Donc 2(x + 1,3) =
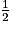 [2(4 − x + 1,3)].
[2(4 − x + 1,3)].
