Signaler une erreur
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019
Imprimer
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019
Exercice 4 (5 points)
En traversant une plaque de verre teintée, un rayon lumineux perd 20 % de son intensité lumineuse. L'intensité lumineuse est exprimée en candela (cd).
On utilise une lampe torche qui émet un rayon d'intensité lumineuse réglée à 400 cd.
On superpose n plaques de verre identiques (n étant un entier naturel) et on désire mesurer l'intensité lumineuse In du rayon à la sortie de la n-ième plaque.
On note I0 = 400 l'intensité lumineuse du rayon émis par la lampe torche avant de traverser les plaques (intensité lumineuse initiale). Ainsi, cette situation est modélisée par la suite (In).
On utilise une lampe torche qui émet un rayon d'intensité lumineuse réglée à 400 cd.
On superpose n plaques de verre identiques (n étant un entier naturel) et on désire mesurer l'intensité lumineuse In du rayon à la sortie de la n-ième plaque.
On note I0 = 400 l'intensité lumineuse du rayon émis par la lampe torche avant de traverser les plaques (intensité lumineuse initiale). Ainsi, cette situation est modélisée par la suite (In).
1. Montrer par un calcul que I1 = 320.
2.
a. Pour tout entier naturel n, exprimer In+1 en fonction de In.
b. En déduire la nature de la suite (In). Préciser sa raison et son premier terme.
c. Pour tout entier naturel n, exprimer In en fonction de n.
3.
On souhaite déterminer le nombre minimal n de plaques à superposer afin que le rayon initial ait perdu au moins 70 % de son intensité lumineuse initiale après sa traversée des plaques.
a. Afin de déterminer le nombre de plaques à superposer, on considère la fonction Python suivante :
def nombrePlaques(J):
I=400 n=0
while I> J:
I = 0.8*I
n = n+1
return n
Préciser, en justifiant, le nombre j de sorte que l'appel nombrePlaques(J) renvoie le nombre de plaques à superposer.
def nombrePlaques(J):
I=400 n=0
while I> J:
I = 0.8*I
n = n+1
return n
Préciser, en justifiant, le nombre j de sorte que l'appel nombrePlaques(J) renvoie le nombre de plaques à superposer.
b. Le tableau suivant donne des valeurs de In. Combien de plaques doit-on superposer ?
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| In | 400 | 320 | 256 | 204,8 | 163,84 | 131,07 | 104,85 | 83,886 |
Corrigé
Exercice 4 :
Une suite est géométrique si et seulement si, pour passer d'un terme au suivant, on multiplie toujours pas un même réel.
Diminuer une quantité de t % revient à multiplier cette quantité par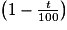 .
.
Diminuer une quantité de t % revient à multiplier cette quantité par
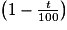 .
.1. 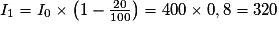
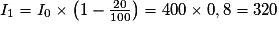
2.
a. Pour tout de n de  ,
, 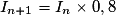 .
.
 ,
, 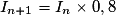 .
.b. La suite (In) est donc géométrique de raison q = 0,8 et de premier terme I0 = 400.
c. Pour tout n de  ,
, 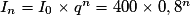 .
.
 ,
, 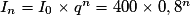 .
.3.
a. 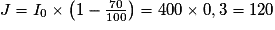 .
.
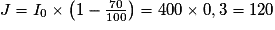 .
.b. On cherche le plus petit entier naturel n tel que In 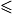 120.
120.
On a I5 > 120 > I6. Donc le plus petit entier naturel n tel que In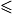 120 est 6.
120 est 6.
Ainsi on devra superposer 6 plaques.
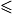 120.
120.On a I5 > 120 > I6. Donc le plus petit entier naturel n tel que In
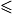 120 est 6.
120 est 6.Ainsi on devra superposer 6 plaques.
Corrigé
Exercice 4 :
Une suite est géométrique si et seulement si, pour passer d'un terme au suivant, on multiplie toujours pas un même réel.
Diminuer une quantité de t % revient à multiplier cette quantité par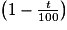 .
.
Diminuer une quantité de t % revient à multiplier cette quantité par
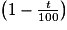 .
.1. 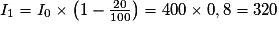
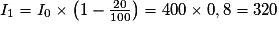
2.
a. Pour tout de n de  ,
, 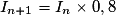 .
.
 ,
, 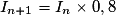 .
.b. La suite (In) est donc géométrique de raison q = 0,8 et de premier terme I0 = 400.
c. Pour tout n de  ,
, 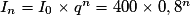 .
.
 ,
, 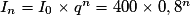 .
.3.
a. 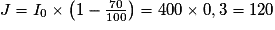 .
.
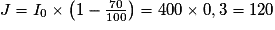 .
.b. On cherche le plus petit entier naturel n tel que In 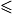 120.
120.
On a I5 > 120 > I6. Donc le plus petit entier naturel n tel que In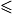 120 est 6.
120 est 6.
Ainsi on devra superposer 6 plaques.
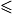 120.
120.On a I5 > 120 > I6. Donc le plus petit entier naturel n tel que In
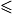 120 est 6.
120 est 6.Ainsi on devra superposer 6 plaques.
Signaler une erreur
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019
Imprimer
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 4, 2019

