Exercice 1 – QCM (5 points)
Pour chacune des questions, une seule des quatre réponses proposées est correcte.
Les questions sont indépendantes.
Pour chaque question, indiquer le numéro de la question et recopier sur la copie la lettre correspondante à la réponse choisie.
Aucune justification n'est demandée mais il peut être nécessaire d'effectuer des recherches au brouillon pour aider à déterminer votre réponse.
Chaque réponse correcte rapporte 1 point. Une réponse incorrecte ou une question sans réponse n'apporte ni ne retire de point.
Les questions sont indépendantes.
Pour chaque question, indiquer le numéro de la question et recopier sur la copie la lettre correspondante à la réponse choisie.
Aucune justification n'est demandée mais il peut être nécessaire d'effectuer des recherches au brouillon pour aider à déterminer votre réponse.
Chaque réponse correcte rapporte 1 point. Une réponse incorrecte ou une question sans réponse n'apporte ni ne retire de point.
Question 1
Pour tout réel x, (ex)3 est égal à :| a) ex × e3 | b) ex+3 | c) e3x | d) ex3 |
Question 2
Pour tout réel x, cos(x + π) est égal à :| a) sin x | b) −cos x | c) cos x | d) −sin x |
Question 3
On souhaite modéliser le niveau de la mer par une suite (Un) de façon que U0 représente le niveau de la mer, en mm, en 2003 et que Un représente le niveau de la mer, en mm, n années après 2003.Selon le site www.notre-planete.info/terre/climatologie_meteo, on constate une hausse assez rapide du niveau de la mer, qu'on estime à 3,3 mm par an depuis 2003.
Pour traduire ce constat, la suite (Un) doit être :
| a) une suite géométrique de raison 3,3. | b) une suite géométrique de raison 1,033. | c) une suite arithmétique de raison 1,033. | d) une suite arithmétique de raison 3,3. |
Question 4
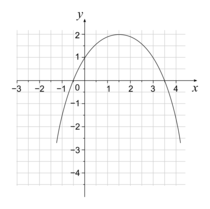
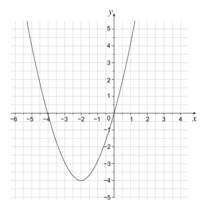
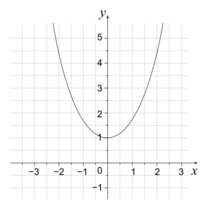
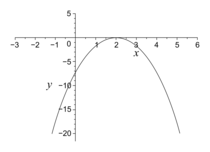
Les figures ci-dessous représentent quatre polynômes du second degré dans un repère orthonormé, et le signe de leur discriminant Δ.Parmi ces propositions, laquelle est juste ?
a)
| b)
| c)
| d)
|
Question 5
Le plan est rapporté à un repère orthonormé.(D) est une droite dont une équation cartésienne est 2x − y + 3 = 0 .
Parmi ces propositions, laquelle est juste ?
| a) La droite (D) passe par le point A de coordonnées (2 ; 1). | b) La droite (D) est dirigée par le vecteur de coordonnées (−1 ; 2). | c) Le vecteur de coordonnées (2 ; −1) est normal à la droite (D). | d) Le point d'intersection de la droite (D) avec l'axe des abscisses a comme coordonnées (0 ; 3). |
Corrigé
Exercice 1 :
Q1 : c.Pour tout x de
 ,
, 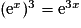 .En effet, pour tous réels a et b,
.En effet, pour tous réels a et b, 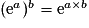 .
.Q2 : b.
Pour tout x de
 , cos(x + π) = −cos(x).
, cos(x + π) = −cos(x).Q3 : d.
Pour tout n de
 , Un+1 = Un + 3,3. Car Un+1 est le niveau de la mer (en mm) l'année suivant l'année (2003 + n).
, Un+1 = Un + 3,3. Car Un+1 est le niveau de la mer (en mm) l'année suivant l'année (2003 + n).Q4 : a.
Soit f définie sur
 par f(x) = ax2 + bx + c, soit Δ le discriminant de f(x) soit (Cf) la courbe représentative de f dans un repère.
par f(x) = ax2 + bx + c, soit Δ le discriminant de f(x) soit (Cf) la courbe représentative de f dans un repère.Δ > 0 si et seulement si (Cf) coupe l'axe des abscisses en deux points distincts.
Δ = 0 si et seulement si (Cf) coupe l'axe des abscisses en un unique point.
Δ < 0 si et seulement si (Cf) ne possède aucun point d'intersection avec l'axe des abscisses.
Q5 : c.
On a (D) : 2x − y + 3 = 0.
La première proposition est fausse car : 2xA − yA + 3 = 2 × 2 − 1+ 3 = 6. Or
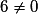 . Donc A n'appartient pas à (D) car les coordonnées de A ne vérifient pas l'équation de (D).
. Donc A n'appartient pas à (D) car les coordonnées de A ne vérifient pas l'équation de (D).La deuxième proposition est fausse. Un vecteur directeur de (D) est
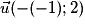 , c'est-à-dire
, c'est-à-dire 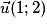 , car pour une droite (d) : ax + by + c = 0, un vecteur directeur de (d) est
, car pour une droite (d) : ax + by + c = 0, un vecteur directeur de (d) est 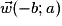 .
.Soit
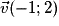 .
. 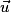 et
et 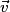 ne sont pas colinéaires car
ne sont pas colinéaires car 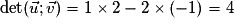 et
et 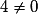 . Donc
. Donc 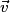 ne peut pas être un vecteur directeur de (D).
ne peut pas être un vecteur directeur de (D).La troisième proposition est juste. On note
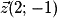 .
. 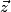 est normal à (D) si et seulement si
est normal à (D) si et seulement si 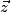 est orthogonal à un vecteur directeur de (D). Et le produit scalaire
est orthogonal à un vecteur directeur de (D). Et le produit scalaire 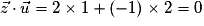 .
.La quatrième proposition est fausse. Soit B(xB ; 0) le point d'intersection de (D) avec l'axe des abscisses, alors les coordonnées de B vérifient l'équation de (D) et 2xB − yB + 3 = 0 donc 2xB− 0 + 3 = 0, soit
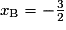 . Ainsi
. Ainsi 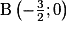 .
.Le point proposé est en fait le point d'intersection de (D) et de l'axe des ordonnées.