I. Qu'est-ce qu'une suite ?
En seconde, le concept de fonction numérique a été défini.• Lorsque l'on observe un phénomène discret, c'est-à-dire que des observations sont effectuées lors des étapes (première étape, deuxième étape, etc.), alors la fonction que l'on peut utiliser pour modéliser l'évolution du phénomène a son ensemble de définition qui est l'ensemble des entiers (ou une partie de 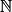 ).
).
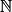 ).
).• Définition : Une fonction numérique dont l'ensemble de définition est 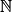 (ou une partie de
(ou une partie de 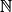 ) est appelée suite numérique.
) est appelée suite numérique.
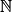 (ou une partie de
(ou une partie de 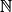 ) est appelée suite numérique.
) est appelée suite numérique.• Exemple : On s'intéresse à la consommation électrique (en MW) en France les journées de juin 2023 à 8 h. On va considérer la fonction c qui à x jours après le 1er juin associe la consommation électrique c(x) en MW en France d'après le site rte-france.com. La variable étant entière et muette, on la note plus souvent n.
On a donc les égalités suivantes :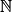 donc c est une suite.
donc c est une suite.
On a donc les égalités suivantes :
- c(0) = 43464
- c(1) = 43237
- etc.
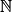 donc c est une suite.
donc c est une suite.• Notations :
- L'image de n par une suite u peut être notée u(n), mais sera très souvent notée un.
- un est le (n + 1)ème terme de la suite u (si u est définie sur
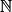 ).
). - Une suite u sera très souvent désignée par (un).
II. Comment démontrer qu'une suite est arithmétique ?
• Définition : On dit qu'une suite (un) définie sur 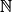 est arithmétique de raison r (r un réel) si, et seulement si, pour tout n de
est arithmétique de raison r (r un réel) si, et seulement si, pour tout n de 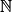 on a : un+1 = un + r. On dit que c'est une relation de récurrence.
on a : un+1 = un + r. On dit que c'est une relation de récurrence.
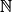 est arithmétique de raison r (r un réel) si, et seulement si, pour tout n de
est arithmétique de raison r (r un réel) si, et seulement si, pour tout n de 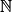 on a : un+1 = un + r. On dit que c'est une relation de récurrence.
on a : un+1 = un + r. On dit que c'est une relation de récurrence.• Exemple : Léonard a emprunté un capital de 3 000 € à sa grand-mère pour acheter un appartement. Pour le remboursement, il choisit de verser 1 % du capital initial de manière mensuelle. Il effectue son premier virement le 16 août 2023. On dit que les intérêts versés sont simples (même somme versée chaque mois). Pour tout entier naturel n, on note cn le capital (en euros) restant à rembourser n mois après le 16 août 2023.
• Démontrons que la suite (cn) est une suite arithmétique (et déterminons ses paramètres : premier terme et raison).
On a c0 = 3 000 car il reste 3 000 euros (capital initial) à rembourser 0 mois après le 16/08/23.
On a c0 = 3 000 car il reste 3 000 euros (capital initial) à rembourser 0 mois après le 16/08/23.
• Calculons ce que représente 1 % du capital initial : 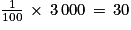 . Léonard verse donc 30 € par mois.
. Léonard verse donc 30 € par mois.
(Ainsi c1 = c0 − 30 = 3 000 − 30 = 2 970).
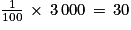 . Léonard verse donc 30 € par mois.
. Léonard verse donc 30 € par mois.(Ainsi c1 = c0 − 30 = 3 000 − 30 = 2 970).
• On a donc pour tout n de  : cn+1 = cn − 30.
: cn+1 = cn − 30.
 : cn+1 = cn − 30.
: cn+1 = cn − 30.• Donc la suite (cn) est arithmétique de raison r = − 30.
Exercice n°2
Exercice n°2
III. Quelle est l'expression du terme général d'une suite arithmétique ?
• Propriété 1 : Si (un) est une suite définie sur 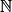 et arithmétique de raison r (r un réel), alors pour tout n de
et arithmétique de raison r (r un réel), alors pour tout n de 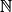 , on a : un = u0 + n × r. On dit que c'est une relation fonctionnelle.
, on a : un = u0 + n × r. On dit que c'est une relation fonctionnelle.
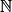 et arithmétique de raison r (r un réel), alors pour tout n de
et arithmétique de raison r (r un réel), alors pour tout n de 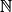 , on a : un = u0 + n × r. On dit que c'est une relation fonctionnelle.
, on a : un = u0 + n × r. On dit que c'est une relation fonctionnelle.• Exemple : Reprenons la situation de Léonard. La suite (cn) est arithmétique de raison r = − 30 et de premier terme c0 = 3 000. Ainsi pour tout n de 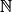 : cn = 3 000 + n × (− 30) = 3 000 − 30n.
: cn = 3 000 + n × (− 30) = 3 000 − 30n.
Exercice n°3
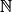 : cn = 3 000 + n × (− 30) = 3 000 − 30n.
: cn = 3 000 + n × (− 30) = 3 000 − 30n.Exercice n°3
• Propriété 2 : Soit (un) une suite définie sur 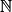 . Si pour tout n de
. Si pour tout n de  , on a : un = x + n × y (avec x et y deux réels), alors (un) est arithmétique de premier terme u0 = x et de raison y.
, on a : un = x + n × y (avec x et y deux réels), alors (un) est arithmétique de premier terme u0 = x et de raison y.
 . Si pour tout n de
. Si pour tout n de  , on a : un = x + n × y (avec x et y deux réels), alors (un) est arithmétique de premier terme u0 = x et de raison y.
, on a : un = x + n × y (avec x et y deux réels), alors (un) est arithmétique de premier terme u0 = x et de raison y.• Exemple : On considère une famille logique de motifs dont les deux premiers sont donnés ici :
Motif n° 1
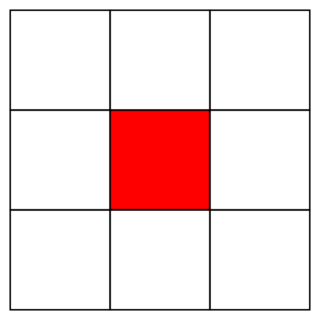 |
Motif n° 2
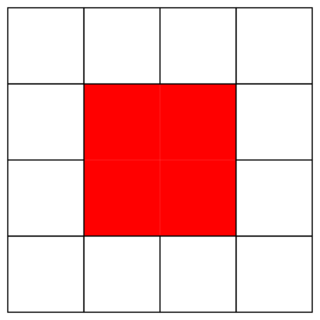 |
• Pour tout entier naturel n, on note bn le nombre de carrés blancs dans le motif n°(n + 1). On observe donc que b0 = 8 et que b1 = 12.
• Le motif n°(n + 1) comporte (n + 3)2 carrés dont (n + 1)2 carrés rouges. Donc le motif n°(n + 1) comporte (n + 3)2 − (n + 1)2 carrés blancs.
Ainsi pour tout entier n de , on a : bn = (n + 3)2 − (n + 1)2
, on a : bn = (n + 3)2 − (n + 1)2
Ainsi pour tout entier n de
 , on a : bn = (n + 3)2 − (n + 1)2
, on a : bn = (n + 3)2 − (n + 1)2 - bn = n2 + 6n + 9 − (n2 + 2n + 1)
- bn = n2 + 6n + 9 − n2 − 2n − 1
- bn = 4n + 8
• On a montré que pour tout entier n de  , bn = x + n × y avec x = 8 et y = 4.
, bn = x + n × y avec x = 8 et y = 4.
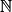 , bn = x + n × y avec x = 8 et y = 4.
, bn = x + n × y avec x = 8 et y = 4.• Donc (bn) est une suite arithmétique de raison r = 4 et de premier terme b0 = 8.
IV. Comment étudier le sens de variation d'une suite arithmétique ?
• Propriété : Soit (un) une suite définie sur 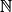 et arithmétique de raison r (r un réel), alors :
et arithmétique de raison r (r un réel), alors :
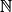 et arithmétique de raison r (r un réel), alors :
et arithmétique de raison r (r un réel), alors :- si r > 0, alors (un) est strictement croissante ;
- si r < 0, alors (un) est strictement décroissante ;
- si r = 0, alors (un) est constante.
• Exemple : Soit (bn) est une suite arithmétique de raison r = 4 et de premier terme b0 = 8.
Comme 4 > 0, alors (bn) est strictement croissante.
Comme 4 > 0, alors (bn) est strictement croissante.
V. Comment représenter graphiquement une suite arithmétique ?
On munit le plan d'un repère, de préférence orthogonal, voire orthonormé.• Définition : Soit (un) une suite définie sur 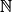 et arithmétique de raison r (r un réel), alors la représentation graphique de la suite est l'ensemble des points M de coordonnées M(n ;un).
et arithmétique de raison r (r un réel), alors la représentation graphique de la suite est l'ensemble des points M de coordonnées M(n ;un).
 et arithmétique de raison r (r un réel), alors la représentation graphique de la suite est l'ensemble des points M de coordonnées M(n ;un).
et arithmétique de raison r (r un réel), alors la représentation graphique de la suite est l'ensemble des points M de coordonnées M(n ;un).• Exemple : Soit (bn) est une suite arithmétique de raison r = 4 et de premier terme b0 = 8.
On a donc pour tout entier n de : bn = 8 + 4n.
: bn = 8 + 4n.
Donc b0 = 8 + 4 × 0 = 8 ; b1 = 8 + 4 × 1 = 12 ; b2 = 8 + 4 × 2 = 16 ; b3 = 8 + 4 × 3 = 30.
Donc on va placer les premiers points de la représentation graphique de la suite (bn) : les points A(0 ;8), B(1 ;12), C(2 ;16) et D(3 ;20).
On a donc pour tout entier n de
 : bn = 8 + 4n.
: bn = 8 + 4n.Donc b0 = 8 + 4 × 0 = 8 ; b1 = 8 + 4 × 1 = 12 ; b2 = 8 + 4 × 2 = 16 ; b3 = 8 + 4 × 3 = 30.
Donc on va placer les premiers points de la représentation graphique de la suite (bn) : les points A(0 ;8), B(1 ;12), C(2 ;16) et D(3 ;20).
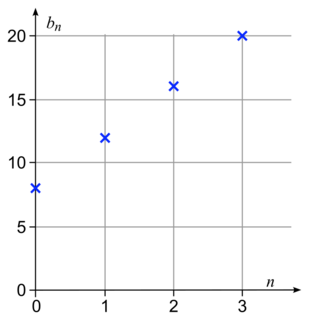 |
• Remarque : On obtient un nuage de points et les points sont alignés. C'est pour cela que lorsqu'un phénomène est modélisé par une suite arithmétique, on parle d'évolution linéaire.
Exercice n°4
Exercice n°4
VI. Comment résoudre un problème de seuil ?
• Soit a, b et c trois réels (et a non nul). Pour résoudre une équation linéaire du premier degré d'inconnue n du type a × n + b = c, on va procéder ainsi :
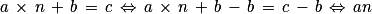
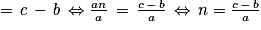
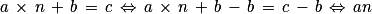
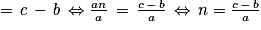
• On devra vérifier que le nombre 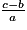 est bien un entier naturel. On peut aussi utiliser un script du type :
est bien un entier naturel. On peut aussi utiliser un script du type :
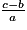 est bien un entier naturel. On peut aussi utiliser un script du type :
est bien un entier naturel. On peut aussi utiliser un script du type : |
Dans ce script :
• u0 est le premier terme de la suite arithmétique ;
• r est la raison de la suite ;
• c est la valeur que l'on souhaite atteindre.
Exemple : On considère une famille logique de motifs dont les deux premiers sont donnés ici :
Motif n° 1
 |
Motif n° 2
 |
• Pour tout entier naturel n, on note bn le nombre de carrés blancs dans le motif n°(n + 1).
• On observe donc que b0 = 8 et que b1 = 12.
• On a montré que pour tout entier naturel n : bn = 4n + 8.
• Est-il possible de trouver un motif dont le nombre de carrés blancs sera égal à 1 492 ?
On doit donc résoudre l'équation : bn = 1 492.
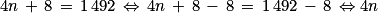
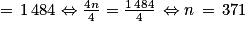
371 est bien un entier. Donc b371 = 1 492. Cela signifie que le motif n°(371 + 1) soit le motif n° 372 comporte exactement 1 492 carrés blancs.
On doit donc résoudre l'équation : bn = 1 492.
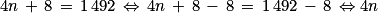
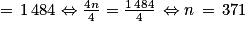
371 est bien un entier. Donc b371 = 1 492. Cela signifie que le motif n°(371 + 1) soit le motif n° 372 comporte exactement 1 492 carrés blancs.
• Remarque : on peut aussi avoir besoin de résoudre des inéquations du type a × n + b > c.
- Si a > 0, alors
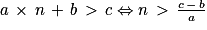
- Si a < 0, alors
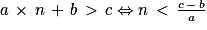
Exercice n°1
On considère la suite l qui à tout nombre entier naturel n lui associe le nombre de lettres l(n) nécessaires pour écrire l'entier. Quelle égalité est fausse ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
l(0) = l0 = 4 car zéro contient quatre lettres
l(1) = l1 = 2 car un contient deux lettres
l(2) = l2 = 4 car deux contient quatre lettres
l(3) = l3 = 5 car trois contient cinq lettres
Donc c'est la réponse C qui était fausse, car elle affirmait l2 = 3.
l(1) = l1 = 2 car un contient deux lettres
l(2) = l2 = 4 car deux contient quatre lettres
l(3) = l3 = 5 car trois contient cinq lettres
Donc c'est la réponse C qui était fausse, car elle affirmait l2 = 3.
Exercice n°2
On dispose d'un très grand nombre de tables rectangulaires et identiques. Sur la largeur d'une table, on peut disposer une seule chaise à chaque bout. Sur la longueur d'une table, on peut disposer deux chaises de chaque côté.
Une table
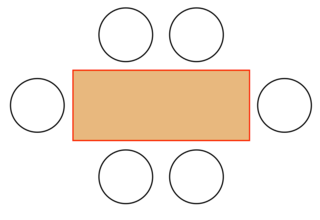 |
Deux tables
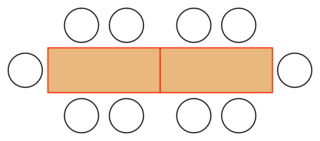 |
Pour tout entier naturel n, on note tn le nombre de places assises dont on dispose en plaçant (n + 1) tables mises bout à bout.
La suite (tn) est arithmétique. Quels sont ses paramètres ?
La suite (tn) est arithmétique. Quels sont ses paramètres ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
t0 est le nombre de places assises dont on dispose en plaçant (0 + 1) tables mises bout à bout, c'est à dire juste une table. On peut placer six personnes. Donc t0 = 6.
À chaque fois que l'on ajoute une table, on peut placer quatre personnes supplémentaires.
On a donc pour tout n de on a : tn+1 = tn + 4.
on a : tn+1 = tn + 4.
Ainsi (tn) est arithmétique de raison r = 4.
Ainsi c'est la réponse A qui est correcte.
À chaque fois que l'on ajoute une table, on peut placer quatre personnes supplémentaires.
On a donc pour tout n de
 on a : tn+1 = tn + 4.
on a : tn+1 = tn + 4.Ainsi (tn) est arithmétique de raison r = 4.
Ainsi c'est la réponse A qui est correcte.
Exercice n°3
On dispose d'un très grand nombre de tables rectangulaires et identiques.
Sur la largeur d'une table, on peut disposer une seule chaise à chaque bout.
Sur la longueur d'une table, on peut disposer deux chaises de chaque côté.
Sur la largeur d'une table, on peut disposer une seule chaise à chaque bout.
Sur la longueur d'une table, on peut disposer deux chaises de chaque côté.
Une table
 |
Deux tables
 |
Pour tout entier naturel n, on note tn le nombre de places assises dont on dispose en utilisant (n + 1) tables mises bout à bout.
On admet que la suite (tn) est arithmétique de raison égale à 4 et de premier terme égal à 6.
Quelle est l'expression du terme général de tn ?
On admet que la suite (tn) est arithmétique de raison égale à 4 et de premier terme égal à 6.
Quelle est l'expression du terme général de tn ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
On sait que si (tn) est une suite définie sur \mathbb{N} et arithmétique de raison r (r un réel), alors pour tout n de 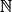 on a : tn = t0 + n × r.
on a : tn = t0 + n × r.
Or ici r = 4 et t0 = 6. Donc pour tout entier naturel n : tn = 4n + 6 = 6+ 4n.
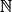 on a : tn = t0 + n × r.
on a : tn = t0 + n × r.Or ici r = 4 et t0 = 6. Donc pour tout entier naturel n : tn = 4n + 6 = 6+ 4n.
Exercice n°4
On admet que pour tout entier naturel n : tn = 4n + 6.
Déterminer le point n'appartenant pas à la représentation graphique de la suite (tn).
Déterminer le point n'appartenant pas à la représentation graphique de la suite (tn).
Cochez la bonne réponse.
| ||
| ||
| ||
|
t0 = 4 × 0 + 6 = 6. Donc le point de coordonnées (0 ;6) appartient à la représentation graphique.
t1 = 4 × 1 + 6 = 10. Donc le point de coordonnées (1 ;10) appartient à la représentation graphique.
t2 = 4 × 2 + 6 = 14. Donc le point de coordonnées (2 ;14) appartient à la représentation graphique. Le point G n'appartient donc pas à la représentation graphique.
t10 = 4 × 10 + 6 = 46. Donc le point de coordonnées (10 ;46) appartient à la représentation graphique.
t1 = 4 × 1 + 6 = 10. Donc le point de coordonnées (1 ;10) appartient à la représentation graphique.
t2 = 4 × 2 + 6 = 14. Donc le point de coordonnées (2 ;14) appartient à la représentation graphique. Le point G n'appartient donc pas à la représentation graphique.
t10 = 4 × 10 + 6 = 46. Donc le point de coordonnées (10 ;46) appartient à la représentation graphique.
Exercice n°5
On dispose d'un très grand nombre de tables rectangulaires et identiques. Sur la largeur d'une table, on peut disposer une seule chaise à chaque bout. Sur la longueur d'une table, on peut disposer deux chaises de chaque côté.
Une table
 |
Deux tables
 |
Pour tout entier naturel n, on note tn le nombre de places assises dont on dispose en utilisant (n + 1) tables mises bout à bout.
On admet que pour tout entier naturel n : tn = 4n + 6.
De combien de tables a-t-on besoin si l'on souhaite asseoir 126 personnes ?
On admet que pour tout entier naturel n : tn = 4n + 6.
De combien de tables a-t-on besoin si l'on souhaite asseoir 126 personnes ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
On doit résoudre l'équation tn = 126.
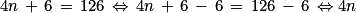
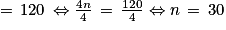
30 est bien un entier. On a donc : t30 = 126. Donc en utilisant (30 + 1) tables mises bout à bout, soit 31 tables, on pourra asseoir 126 personnes.
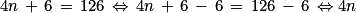
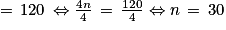
30 est bien un entier. On a donc : t30 = 126. Donc en utilisant (30 + 1) tables mises bout à bout, soit 31 tables, on pourra asseoir 126 personnes.

