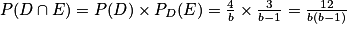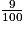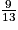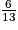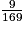I. Comment calculer les différents types de fréquences ?
On considère un tableau croisé d'effectifs.
Fréquence
• Une fréquence se calcule en utilisant une case intérieure (hors dernière ligne et hors dernière colonne souvent nommée « Total »). C'est le quotient de la valeur de la case intérieure par l'effectif total.
• Exemple : catégorisation des Lillois.
- Population : la ville de Lille en 2019.
- Individus : habitants.
- Premier caractère étudié : sexe.
- Second caractère étudié : âge.
| | Hommes | Femmes | Total |
|---|---|---|---|
| Strictement moins de 30 ans | 58 382 | 61 775 | 120 157 |
| Plus de 30 ans | 54 835 | 59 483 | 114 318 |
| Total | 113 217 | 121 258 | 234 475 |
• Calculons la fréquence de femmes de plus de 30 ans dans la population lilloise en 2019. Cette fréquence est égale à 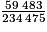 soit environ 0,2537 (ou encore environ 25,37 %).
soit environ 0,2537 (ou encore environ 25,37 %).
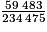 soit environ 0,2537 (ou encore environ 25,37 %).
soit environ 0,2537 (ou encore environ 25,37 %).Fréquence marginale
• Une fréquence marginale se calcule en utilisant une « marge » (dernière ligne ou dernière colonne souvent nommée « Total »). C'est le quotient de la valeur de la case marginale visée par l'effectif total.
• Exemple : Calculons la fréquence de femmes dans la population lilloise en 2019. C'est bien une fréquence marginale que l'on doit calculer. Elle est égale à 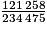 soit environ 51,71 %.
soit environ 51,71 %.
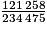 soit environ 51,71 %.
soit environ 51,71 %.Fréquence conditionnelle
• Une fréquence conditionnelle se calcule en utilisant une case intérieure et une « marge » (dernière ligne ou dernière colonne souvent nommée « Total »). C'est le quotient de la valeur de la case visée par la valeur de la case marginale.
• Exemple : Calculons la fréquence d'hommes parmi les habitants de plus de 30 ans. C'est bien une fréquence conditionnelle que l'on doit calculer (puisque l'ensemble de référence n'est plus la population totale, mais une sous-population : les habitants de plus de 30 ans). Elle est égale à 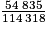 soit environ 47,97 %.Exercice n°1
soit environ 47,97 %.Exercice n°1
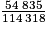 soit environ 47,97 %.Exercice n°1
soit environ 47,97 %.Exercice n°1II. Quel lien existe-t-il entre les fréquences et les probabilités ?
• Dans le cas d'un tirage aléatoire dans une population finie, la fréquence peut être identifiée à une probabilité. En effet, on estime que choisir au hasard un individu dans une population est une situation d'équiprobabilité : chaque individu de la population a autant de chance d'être choisi qu'un autre.
• Exemple : On choisit au hasard un habitant de Lille en 2019. On note H l'événement « l'habitant choisi est un homme » et T l'événement « l'habitant choisi a plus de 30 ans ». Alors la probabilité de H est égale à la fréquence d'hommes dans la population lilloise.
Ainsi 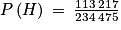
L'événement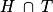 peut être décrit par « l'habitant choisi est un homme de plus de 30 ans ».
peut être décrit par « l'habitant choisi est un homme de plus de 30 ans ».
On a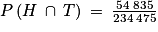 Exercice n°2
Exercice n°2
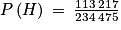
L'événement
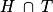 peut être décrit par « l'habitant choisi est un homme de plus de 30 ans ».
peut être décrit par « l'habitant choisi est un homme de plus de 30 ans ».On a
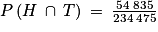 Exercice n°2
Exercice n°2III. Comment calculer une probabilité conditionnelle ?
Lecture d'un arbre
• On considère une expérience aléatoire et deux événements A et B quelconques de probabilités non nulles. L'événement A est réalisé puis l'événement B.
• On peut visualiser la situation en utilisant un arbre pondéré :
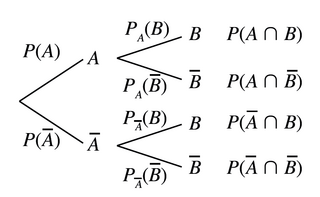 |
• La probabilité de l'événement « B sachant que l'événement A est réalisé », notée PA(B) peut se calculer en utilisant un arbre.
En effet on a :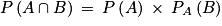 donc
donc 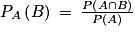 .
.
En effet on a :
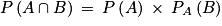 donc
donc 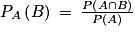 .
.• Par analogie on en déduit que la probabilité de l'événement « A sachant que l'événement B est réalisé », notée PB(A) sera égale à : 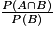 .
.
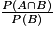 .
.• Remarque : Ainsi les fréquences conditionnelles peuvent être identifiées à des probabilités conditionnelles.Exercice n°3Exercice n°4
IV. Comment construire un arbre de probabilité ?
• Exemple : Une compagnie d'assurance auto propose deux types de contrat :
- un contrat « de base ».
- un contrat « Tous risques » ;
• En consultant le fichier clients de la compagnie, on recueille les données suivantes :
- 60 % des clients possèdent un véhicule récent (moins de 5 ans). Les autres clients ont un véhicule ancien ;
- parmi les clients possédant un véhicule récent, 70 % ont souscrit au contrat « Tous risques » ;
- parmi les clients possédant un véhicule ancien, 50 % ont souscrit au contrat « Tous risques ».
• On considère un client choisi au hasard. On note les événements suivants :
- R « le client possède un véhicule récent » ;
- T « le client a souscrit au contrat "Tous risques" ».
• En décryptant l'énoncé, on a :
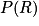 = 60 % = 0,60
= 60 % = 0,60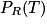 = 70 % = 0,70
= 70 % = 0,70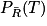 = 50 % = 0,50
= 50 % = 0,50
• Or, on sait que pour tout événement A :
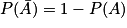
- Donc
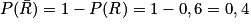 .
.
• De la même manière pour tout événement A et B (B non impossible) :
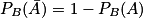
- Donc
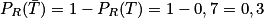 .
.
• De la même manière, on a 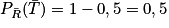 .
.
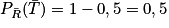 .
.• Par rapport aux probabilités connues, on peut alors construire l'arbre pondéré suivant :
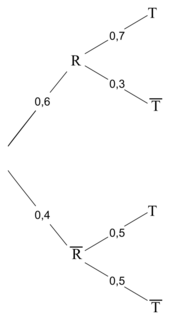 |
V. Comment montrer que deux événements sont indépendants ?
• Propriété : Intuitivement, deux événements sont indépendants si la réalisation de l'un de ces événements n'influe pas sur la probabilité de l'autre. On doit donc avoir : 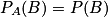 .
.
A et B sont donc indépendants si et seulement si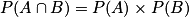 .
.
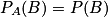 .
.A et B sont donc indépendants si et seulement si
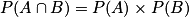 .
.• Remarque : Attention à ne pas confondre incompatibles et indépendants :
- A et B sont donc incompatibles si et seulement si
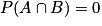 ;
; - A et B sont donc indépendants si et seulement si
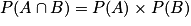 .
.
Quels sont les groupes sanguins donneurs et receveur universel ?
En France, le groupe A est le plus représenté (38 %). Viennent ensuite les groupes O (36 %), B (8 %), A− (7 %), O− (6 %), AB (3 %), B− (1 %), AB− (1 %) parmi les plus rares. Cette répartition est propre à la France. Elle varie selon les pays, les continents. « En Amérique du Sud, par exemple, le groupe O est de loin le plus répandu », affirme l'EFS. Le Pérou compte 71 % de sa population comme étant de groupe O. Le plus rare restant le groupe AB. En Inde, 40 % de la population est de groupe B. Ce n'est pas parce que le groupe A+ est le plus répandu en France qu'il n'est pas le plus recherché. Au contraire. C'est justement parce qu'il est très commun au sein de la population qu'il permet de sauver de nombreuses vies. Le groupe O− est considéré comme un « donneur universel », c'est-à-dire qu'il peut donner son sang à n'importe quel autre groupe. À l'inverse, le groupe AB+ est un receveur universel.• On peut construire le tableau à double entrée suivant représentant la répartition des différents groupes sanguins pour un groupe de 100 personnes en France.
| | A | B | O | AB | Total |
|---|---|---|---|---|---|
| Rhésus + | 38 | 8 | 36 | 3 | 85 |
| Rhésus − | 7 | 1 | 6 | 1 | 15 |
| Total | 45 | 9 | 42 | 4 | 100 |
• Soit R l'événement « le rhésus est positif » et soit A l'événement « le groupe est A ».
VI. Comment modéliser une succession d'événements ?
On utilisera un arbre pondéré avec autant de niveaux que de réalisation d'événements.
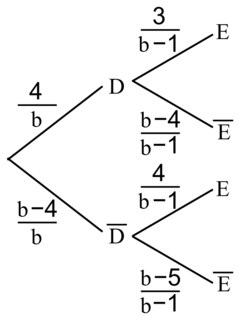
• Exemple : Soit b un entier naturel strictement supérieur à 4. Une boîte opaque contient b billes identiques au toucher : 4 billes sont orange et les autres sont vertes. On va tirer au hasard successivement et sans remise deux billes de la boîte. On note les événements :
- D : « la première bille tirée est orange »
- E : « la seconde bille tirée est orange »
• On va donc modéliser la situation à l'aide d'un arbre pondéré à deux niveaux (car il y a deux tirages).
 |
Exercice n°1
On considère le tableau suivant concernant la population française en 2019.
Est-il vrai qu'il y a au moins 60 % de femmes chez les plus de 65 ans ?
| | Hommes | Femmes | Total |
|---|---|---|---|
| Strictement moins de 20 ans | 8 248 370 | 7 874 268 | 16 122 638 |
| Entre 20 ans et 64 ans (inclus) | 18 435 872 | 19 120 945 | 37 556 817 |
| Plus de 65 ans | 5 712 200 | 7 596 748 | 13 308 948 |
| Total | 32 396 442 | 34 591 961 | 66 988 403 |
Est-il vrai qu'il y a au moins 60 % de femmes chez les plus de 65 ans ?
Cochez la bonne réponse.
| ||
| ||
|
Pour vérifier, on doit calculer la fréquence de femmes parmi les personnes de plus de 65 ans. C'est une fréquence conditionnelle.
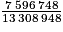
Soit environ 57,08 %. Or 57,08<60. Ainsi il est incorrect d'affirmer qu'il y a au moins 60 % de femmes chez les plus de 65 ans.
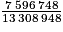
Soit environ 57,08 %. Or 57,08<60. Ainsi il est incorrect d'affirmer qu'il y a au moins 60 % de femmes chez les plus de 65 ans.
Exercice n°2
On considère le tableau suivant concernant la population française en 2019.
On choisit au hasard une personne en France en 2019.
On note F : « la personne est une femme » et V : « la personne a strictement moins de 20 ans ».
Calculer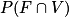 .
.
| | Hommes | Femmes | Total |
|---|---|---|---|
| Strictement moins de 20 ans | 8 248 370 | 7 874 268 | 16 122 638 |
| Entre 20 ans et 64 ans (inclus) | 18 435 872 | 19 120 945 | 37 556 817 |
| Plus de 65 ans | 5 712 200 | 7 596 748 | 13 308 948 |
| Total | 32 396 442 | 34 591 961 | 66 988 403 |
On choisit au hasard une personne en France en 2019.
On note F : « la personne est une femme » et V : « la personne a strictement moins de 20 ans ».
Calculer
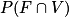 .
. Cochez la bonne réponse.
| ||
| ||
| ||
|
Calculer 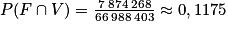 .
.
Ainsi la probabilité que la personne choisie soit une femme de moins de 20 ans est environ égale à 11,75 %.
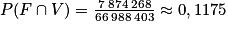 .
.Ainsi la probabilité que la personne choisie soit une femme de moins de 20 ans est environ égale à 11,75 %.
Exercice n°3
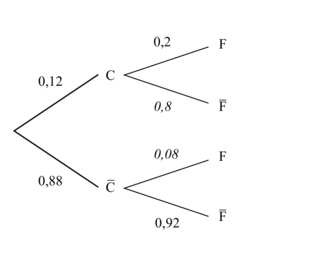
On considère l'arbre pondéré suivant :
 |
À quoi est égale 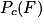 ?
?
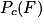 ?
? Cochez la bonne réponse.
| ||
| ||
|
On cherche la probabilité que l'événement F se réalise sachant que l'événement C s'est déjà réalisé.
Par lecture de l'arbre on trouve que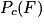 = 0,2.
= 0,2.
Par lecture de l'arbre on trouve que
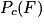 = 0,2.
= 0,2.Exercice n°4
On estime que dans la Métropole européenne de Lille, on a 1 % des conducteurs contrôlés par la police qui sont réellement en état d'ébriété. Une entreprise a mis au point un nouvel éthylotest et, après avoir réalisé 10 000 essais dans les conditions réalistes, affirme que :
On choisit un des 10 000 essais au hasard, calculer la probabilité que le conducteur était en état d'ébriété sachant que le test était positif.
- si un conducteur n'est pas en état d'ébriété alors le test sera négatif dans 96 % des cas ;
- si un conducteur est en état d'ébriété alors le test sera positif dans 98 % des cas.
| | Ébriété | Pas ébriété | Total |
|---|---|---|---|
| Positif | 98 | 396 | 494 |
| Négatif | 2 | 9 504 | 9 506 |
| Total | 100 | 9 900 | 10 000 |
On choisit un des 10 000 essais au hasard, calculer la probabilité que le conducteur était en état d'ébriété sachant que le test était positif.
Cochez la bonne réponse.
| ||
| ||
| ||
|
On calcule alors grâce au tableau :
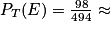 19,84 %
19,84 %
L'éthylotest mis au point n'est donc pas de bonne qualité, car lorsque le test est positif la personne n'est réellement en état d'ébriété que dans environ un cas sur cinq ! On peut aussi utiliser la formule du cours :
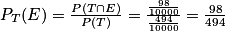
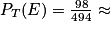 19,84 %
19,84 %L'éthylotest mis au point n'est donc pas de bonne qualité, car lorsque le test est positif la personne n'est réellement en état d'ébriété que dans environ un cas sur cinq ! On peut aussi utiliser la formule du cours :
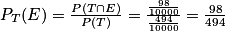
Exercice n°5
On lance un dé équilibré sur une surface plane. On considère I l'événement « obtenir un entier impair » et T : « obtenir un multiple de trois ».
Les événements I et T sont :
Les événements I et T sont :
Cochez la bonne réponse.
| ||
| ||
|
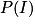 =
= 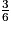 =
= 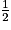
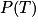 =
= 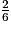 =
= 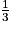
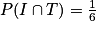
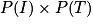 =
= 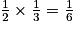
On a
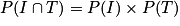 et
et 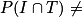 0. Ainsi les événements I et T sont indépendants.
0. Ainsi les événements I et T sont indépendants.Exercice n°6
On considère une urne contenant 10 boules rouges et 3 boules bleues. On tire successivement avec remise deux boules dans l'urne (avec remise signifie que l'on replace la première boule dans l'urne après avoir regardé sa couleur).
Calculer la probabilité que les deux boules tirées soient bleues.
Calculer la probabilité que les deux boules tirées soient bleues.
Cochez la bonne réponse.
| ||
| ||
| ||
|
Soit A : « la première boule tirée est bleue ».
Soit B : « la seconde boule tirée est bleue ».
On a :
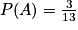
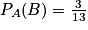
puisqu'il s'agit d'un tirage avec remise.
On a donc :
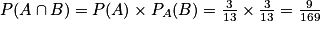
On peut aussi affirmer que, comme le tirage de la première boule n'influe pas sur le tirage de la seconde boule, les événements A et B sont indépendants. Et donc on a :
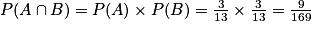
Soit B : « la seconde boule tirée est bleue ».
On a :
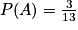
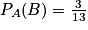
puisqu'il s'agit d'un tirage avec remise.
On a donc :
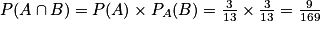
On peut aussi affirmer que, comme le tirage de la première boule n'influe pas sur le tirage de la seconde boule, les événements A et B sont indépendants. Et donc on a :
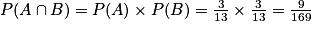
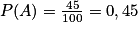
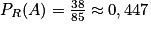
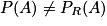 donc les événements A et R ne sont pas indépendants.
donc les événements A et R ne sont pas indépendants.