Consulter le programme
Préambule
L'ensemble des disciplines scientifiques concourt à la compréhension du monde, de son organisation, de son fonctionnement et des lois qui le régissent. Elles permettent aussi de maîtriser les outils et technologies proprement humains. L'histoire des sciences raconte une aventure de l'esprit humain, lancé dans une exploration du monde (la science pour savoir) et dans une action sur le monde (la science pour faire).Le développement des sciences et des technologies a profondément modifié les conditions de vie des êtres humains et les sociétés dans lesquelles ils vivent. Cela s'est traduit par d'importants progrès, dans les domaines de l'alimentation, de la santé, de la communication, des transports, etc. Grâce à ses inventions, l'être humain a désormais les moyens d'agir sur son environnement immédiat. Par son impact, l'espèce humaine modifie également les équilibres à l'échelle globale de la planète. La présence humaine modifie le climat ; ses déchets s'accumulent et son utilisation des ressources naturelles est massive. Si l'espèce humaine n'est pas la première forme de vie à transformer la planète, c'est sans aucun doute la première qui s'en préoccupe.
Grâce, notamment, à l'approche scientifique, l'être humain dispose des outils intellectuels nécessaires pour devenir un acteur conscient et responsable de la relation au monde et de la transformation des sociétés. L'approche scientifique nourrit le jugement critique et rencontre des préoccupations d'ordre éthique. Ainsi, c'est de façon rationnellement éclairée que chacun doit être en mesure de participer à la prise de décisions, individuelles et collectives, locales ou globales.
La science construit peu à peu un corpus de connaissances grâce à des méthodes spécifiques : elle élabore un ensemble de théories, établit des lois, invente des concepts, découvre des mécanismes ; cet ensemble se perfectionne par la confrontation à des faits nouvellement connus, souvent en lien avec l'évolution des techniques. Le savoir scientifique est une construction collective qui a une histoire. Il est fondé sur le raisonnement rationnel et la recherche de causes matérielles ; il se développe parfois en réfutation des intuitions premières au-delà desquelles le scientifique doit s'aventurer.
La compréhension de l'histoire des savoirs scientifiques et de leur mode de construction, la pratique véritable d'une démarche scientifique (y compris dans sa dimension concrète) développent des qualités de l'esprit utiles à tous. Ainsi, en fréquentant la science, chacun développe-t-il son intelligence, sa curiosité, sa raison, son humilité devant les faits et les idées pour enrichir son savoir.
Le but essentiel de l'enseignement scientifique est de dispenser une formation scientifique générale pour tous les élèves, tout en offrant un point d'appui pour ceux qui poursuivent et veulent poursuivre des études scientifiques. Il ne vise pas à construire un savoir encyclopédique mais cherche plutôt à atteindre trois buts intimement liés :
- contribuer à faire de chaque élève une personne lucide, consciente de ce qu'elle est, de ce qu'est le monde et de ce qu'est sa relation au monde ;
- contribuer à faire de chaque élève un citoyen ou une citoyenne responsable, qui connaît les conséquences de ses actions sur le monde et dispose des outils nécessaires pour les contrôler ;
- contribuer au développement en chaque élève d'un esprit rationnel, autonome et éclairé, capable d'exercer une analyse critique face aux fausses informations et aux rumeurs.
Programme
Pour atteindre les objectifs définis en préambule, ce programme précise d'une part des objectifs généraux de formation et présente d'autre part un ensemble d'objectifs thématiques dont les contenus sont largement interdisciplinaires.
Les premiers ont pour but d'aider les élèves à cerner ce que la connaissance scientifique a de spécifique, dans ses pratiques, dans ses méthodes d'élaboration et dans ses enjeux de société. Les objectifs thématiques visent à consolider la culture scientifique des élèves tout en leur fournissant les éléments d'une pratique autonome du raisonnement scientifique dans des contextes variés.
Ces deux aspects sont complémentaires. Les professeurs décident comment satisfaire aux objectifs de formation générale en traitant les contenus de chaque thème. Ils doivent veiller à respecter un juste équilibre entre ces deux composantes de l'enseignement.
Les objectifs généraux de formation et les suggestions pédagogiques qui suivent concernent les deux années du cycle terminal dont les programmes constituent un ensemble cohérent. Certaines thématiques aux enjeux particulièrement importants (climat, énergie, biodiversité) sont abordées dans les programmes des deux années du cycle terminal.
Les premiers ont pour but d'aider les élèves à cerner ce que la connaissance scientifique a de spécifique, dans ses pratiques, dans ses méthodes d'élaboration et dans ses enjeux de société. Les objectifs thématiques visent à consolider la culture scientifique des élèves tout en leur fournissant les éléments d'une pratique autonome du raisonnement scientifique dans des contextes variés.
Ces deux aspects sont complémentaires. Les professeurs décident comment satisfaire aux objectifs de formation générale en traitant les contenus de chaque thème. Ils doivent veiller à respecter un juste équilibre entre ces deux composantes de l'enseignement.
Les objectifs généraux de formation et les suggestions pédagogiques qui suivent concernent les deux années du cycle terminal dont les programmes constituent un ensemble cohérent. Certaines thématiques aux enjeux particulièrement importants (climat, énergie, biodiversité) sont abordées dans les programmes des deux années du cycle terminal.
Objectifs généraux de formation
L'enseignement scientifique cherche à développer des compétences générales par la pratique de la réflexion scientifique. Les objectifs ci-dessous énoncés constituent une dimension essentielle de l'enseignement scientifique et ne doivent pas être négligés au profit du seul descriptif thématique. Ils sont regroupés autour de trois idées, d'ailleurs liées entre elles.
Comprendre la nature du savoir scientifique et ses méthodes d'élaboration
Le savoir scientifique résulte d'une construction rationnelle. Il se distingue d'une croyance ou d'une opinion. Il s'appuie sur l'analyse de faits extraits de la réalité complexe ou produits au cours d'expériences. Il cherche à expliquer la réalité par des causes matérielles.Le savoir scientifique résulte d'une longue construction collective jalonnée d'échanges d'arguments, de controverses parfois vives. C'est lentement qu'une certitude raisonnable s'installe et se précise, au gré de la prise en compte de faits nouveaux, souvent en lien avec les progrès techniques. Ce long travail intellectuel met en jeu l'énoncé d'hypothèses dont on tire des conséquences selon un processus logique. Ces modalités sont d'ailleurs en partie variables selon les disciplines concernées.
Dans le cadre de l'enseignement scientifique, il s'agit donc, en permanence, d'associer l'acquisition de quelques savoirs et savoir-faire exigibles à la compréhension de leur nature et de leur construction.
Identifier et mettre en œuvre des pratiques scientifiques
Au cours de son activité de production du savoir, le scientifique met en œuvre un certain nombre de pratiques qui, si elles ne sont pas spécifiques de son travail, en sont néanmoins des aspects incontournables.Quelques mots-clés permettent de les présenter : observer, décrire, mesurer, quantifier, calculer, imaginer, modéliser, simuler, raisonner, prévoir le futur ou remonter dans le passé.
Cet enseignement contribue au développement des compétences langagières orales à travers notamment la pratique de l'argumentation. Celle-ci conduit à préciser sa pensée et à expliciter son raisonnement de manière à convaincre.
Dans le cadre de l'enseignement scientifique, il s'agit, chaque fois que l'on met en œuvre une authentique pratique scientifique, de l'expliciter et de prendre conscience de sa nature.
Identifier et comprendre les effets de la science sur les sociétés et sur l'environnement
Les sociétés modernes sont profondément transformées par la science et ses applications technologiques. Leurs effets touchent l'alimentation (agriculture et agroalimentaire), la santé (médecine), les communications (transports, échange d'information), l'apprentissage et la réflexion (intelligence artificielle), la maîtrise des risques naturels et technologiques, la protection de l'environnement, etc.La compréhension de ces transformations est indispensable à la prise de décision ; elle distingue l'approche purement scientifique d'autres approches (économiques, éthiques, etc.).
De même, les activités humaines exercent sur l'environnement des effets que la science permet de comprendre et de contrôler. Les conséquences de l'activité humaine sur l'environnement et leur contrôle seront particulièrement développées dans le programme de terminale.
Dans le cadre de l'enseignement scientifique, il s'agit de faire comprendre à chacun en quoi la culture scientifique est aujourd'hui indispensable pour saisir l'évolution des sociétés comme celle de l'environnement et de contrôler cette évolution.
Cet enseignement peut être également mis en relation avec le programme d'enseignement moral et civique de la classe de première qui propose des objets d'étude sur la bioéthique et sur la responsabilité environnementale.
Suggestions pédagogiques
Si les objectifs généraux ou thématiques sont clairement identifiés dans le programme, la manière de les atteindre relève de la liberté pédagogique du professeur ou de l'équipe de professeurs. Ce paragraphe ne limite nullement cette liberté pédagogique ni n'en canalise l'expression. Cependant, quelques principes pédagogiques généraux méritent d'être pris en compte pour atteindre les objectifs fixés.
Un enseignement en prise avec le réel complexe
Le scientifique rend intelligible le monde en déchiffrant la réalité complexe, dont il extrait des éléments qu'il analyse et dont il élucide les interactions. Il est néanmoins opportun de saisir une ou des occasion(s) de montrer la complexité du réel lui-même. Une manière privilégiée de le faire consiste à travailler hors des murs de la classe ou de l'établissement (terrain naturel, laboratoire, entreprise, musée, etc.).La prise en compte de la complexité impose aussi le croisement des approches de plusieurs disciplines ce qui se traduit par le caractère interdisciplinaire de cet enseignement (y compris en dehors du champ scientifique). La rubrique Histoire, enjeux, débats offre des occasions de collaborations variées.
Une place particulière pour les mathématiques
Selon Galilée, le grand livre de la Nature est écrit en langage mathématique. C'est dans cet esprit que les mathématiques trouvent leur place dans ce programme d'enseignement scientifique. De surcroît, l'omniprésence (quoique souvent invisible) des mathématiques dans la vie quotidienne impose aujourd'hui à tout individu de disposer de savoirs et de savoir-faire mathématiques pour réussir pleinement sa vie personnelle, professionnelle et sociale. Le traitement des thèmes figurant au programme permet de présenter des méthodes, modèles et outils mathématiques utilisés pour décrire et expliquer la réalité complexe du monde, mais aussi pour prédire ses évolutions. Parallèlement, le programme offre de nombreuses occasions de confronter les élèves à une pratique effective des mathématiques dans des contextes issus d'autres disciplines. Cette pratique leur permet à la fois de consolider, dans des contextes nouveaux, des compétences de calcul, de raisonnement logique et de représentation et d'exercer leur esprit critique en interrogeant les résultats d'un modèle mathématique.Une place réservée à l'observation et l'expérience en laboratoire
Si des études documentaires ou la résolution d'exercices permettent la mise en œuvre d'une démarche scientifique, la pratique expérimentale des élèves est essentielle. En particulier, il est bienvenu, chaque fois que possible, de créer les conditions permettant un travail de laboratoire fondé sur diverses formes de manipulations et d'observations. Ainsi, l'élève se livre lui-même à la confrontation entre faits et idées et comprend, en la pratiquant, la construction du savoir scientifique.Une place importante pour l'histoire raisonnée des sciences
L'une des manières de comprendre comment se construit le savoir scientifique est de retracer le cheminement effectif de sa construction au cours de l'histoire des sciences. Il ne s'agit pas de donner à l'élève l'illusion qu'il trouve en quelques minutes ce qui a demandé le travail de nombreuses générations de chercheurs, mais plutôt, en se focalisant sur un petit nombre d'étapes bien choisies de l'histoire des sciences, de faire comprendre le rôle clé joué par certaines découvertes. Le rôle prépondérant joué parfois par tel ou tel chercheur sera souligné. Ce sera aussi l'occasion de montrer que l'histoire du savoir scientifique est une aventure humaine. Des controverses, parfois dramatiques, agitent la communauté scientifique. Ainsi, peu à peu, le savoir progresse et se précise.Un usage explicité des outils numériques
Des outils numériques variés trouvent des applications dans le cadre de l'enseignement scientifique : logiciels de calcul ou de simulation, environnements de programmation, logiciels tableurs, etc. Il convient d'associer leur utilisation par les élèves à la compréhension au moins élémentaire de leur nature et de leur fonctionnement.Objectifs thématiques
La suite du programme se présente comme une succession de thèmes. Ces thèmes sont au service des trois grands objectifs de formation (comprendre la nature du savoir scientifique et ses modes d'élaboration, identifier et mettre en œuvre des pratiques scientifiques, identifier et comprendre les effets de la science sur les sociétés et l'environnement). Sa structure est explicitée ci-dessous.
La rubrique Histoire, enjeux, débats établit d'une part quelques éléments historiques en rapport avec la thématique et identifie d'autre part des liens entre le thème et quelques questions socialement vives (économiques, éthiques, etc.). Il est demandé que dans chaque thème, la manière d'aborder les attendus fasse une place à au moins l'un des items de cette liste. Par exemple, on peut choisir de traiter un point selon une démarche historique, mettre l'accent sur ses implications éthiques, etc.
Une disposition en colonnes indique des savoirs et savoir-faire exigibles. Ce sont des objectifs précisément identifiés (notamment en vue de l'évaluation). Ils laissent au professeur ou à l'équipe de professeurs toute latitude pour construire la démarche. Cette double colonne indique les attendus spécifiques des thèmes. L'objectif de l'enseignement est à la fois de construire ces attendus, de former l'esprit et d'atteindre les objectifs généraux listés plus haut.
La rubrique Prérequis et limites montre comment sont mobilisés des acquis des classes antérieures et explicite des limites pour préciser les exigences du programme.
La rubrique Histoire, enjeux, débats établit d'une part quelques éléments historiques en rapport avec la thématique et identifie d'autre part des liens entre le thème et quelques questions socialement vives (économiques, éthiques, etc.). Il est demandé que dans chaque thème, la manière d'aborder les attendus fasse une place à au moins l'un des items de cette liste. Par exemple, on peut choisir de traiter un point selon une démarche historique, mettre l'accent sur ses implications éthiques, etc.
Une disposition en colonnes indique des savoirs et savoir-faire exigibles. Ce sont des objectifs précisément identifiés (notamment en vue de l'évaluation). Ils laissent au professeur ou à l'équipe de professeurs toute latitude pour construire la démarche. Cette double colonne indique les attendus spécifiques des thèmes. L'objectif de l'enseignement est à la fois de construire ces attendus, de former l'esprit et d'atteindre les objectifs généraux listés plus haut.
La rubrique Prérequis et limites montre comment sont mobilisés des acquis des classes antérieures et explicite des limites pour préciser les exigences du programme.
I. Une longue histoire de la matière
L'immense diversité de la matière dans l'Univers se décrit à partir d'un petit nombre de particules élémentaires qui se sont organisées de façon hiérarchisée, en unités de plus en plus complexes, depuis le Big Bang jusqu'au développement de la vie.
Histoire, enjeux et débats
De Fraunhofer à Bethe : les éléments dans les étoiles.Hooke, Schleiden et Schwann : de la découverte de la cellule à la théorie cellulaire. Becquerel, Marie Curie : la découverte de la radioactivité, du radium.
Industrie des métaux et du verre.
1. Un niveau d'organisation : les éléments chimiques
Comment, à partir du seul élément hydrogène, la diversité des éléments chimiques est-elle apparue ? Aborder cette question nécessite de s'intéresser aux noyaux atomiques et à leurs transformations. Cela fournit l'occasion d'introduire un modèle mathématique d'évolution discrète.
Savoirs
Les noyaux des atomes de la centaine d'éléments chimiques stables résultent de réactions nucléaires qui se produisent au sein des étoiles à partir de l'hydrogène initial. La matière connue de l'Univers est formée principalement d'hydrogène et d'hélium alors que la Terre est surtout constituée d'oxygène, d'hydrogène, de fer, de silicium, de magnésium et les êtres vivants de carbone, hydrogène, oxygène et azote.Savoir-faire
Produire et analyser différentes représentations graphiques de l'abondance des éléments chimiques (proportions) dans l'Univers, la Terre, les êtres vivants.L'équation d'une réaction nucléaire stellaire étant fournie, reconnaître si celle-ci relève d'une fusion ou d'une fission.
Savoirs
Certains noyaux sont instables et se désintègrent (radioactivité).L'instant de désintégration d'un noyau radioactif individuel est aléatoire.
La demi-vie d'un noyau radioactif est la durée nécessaire pour que la moitié des noyaux initialement présents dans un échantillon macroscopique se soit désintégrée.
Cette demi-vie est caractéristique du noyau radioactif.
Savoir-faire
Calculer le nombre de noyaux restants au bout de n demi-viesEstimer la durée nécessaire pour obtenir une certaine proportion de noyaux restants. Utiliser une représentation graphique pour déterminer une demi-vie.
Utiliser une décroissance radioactive pour une datation (exemple du carbone 14).
Prérequis et limites
Les notions, déjà connues, de noyaux, d'atome, d'élément chimique et de réaction nucléaire sont remobilisées. Aucune connaissance n'est exigible sur les différents types de radioactivité. L'évolution du nombre moyen de noyaux restants au cours d'une désintégration radioactive se limite au cas de durées discrètes, multiples entiers de la demi-vie. Aucun formalisme sur la notion de suite n'est exigible.Les fonctions exponentielle et logarithme ne font pas partie des connaissances attendues.
2. Des édifices ordonnés : les cristaux
L'organisation moléculaire étant déjà connue, ce thème aborde une autre formed'organisation de la matière : l'état cristallin (qui revêt une importance majeure, tant pour la connaissance de la nature - minéraux et roches, squelettes, etc. - que pour ses applications techniques). La compréhension de cette organisation au travers des exemples choisis mobilise des connaissances sur la géométrie du cube. Elle fournit l'occasion de développer des compétences de représentation dans l'espace et de calculs de volumes.
Savoirs
Le chlorure de sodium solide (présent dans les roches, ou issu de l'évaporation de l'eau de mer) est constitué d'un empilement régulier d'ions : c'est l'état cristallin.Savoir-faire
Utiliser une représentation 3D informatisée du cristal de chlorure de sodium.Relier l'organisation de la maille au niveau microscopique à la structure du cristal au niveau macroscopique.
Savoirs
Plus généralement, une structure cristalline est définie par une maille élémentaire répétée périodiquement. Un type cristallin est défini par la forme géométrique de la maille, la nature et la position dans cette maille des entités qui le constituent.Les cristaux les plus simples peuvent être décrits par une maille cubique que la géométrie du cube permet de caractériser. La position des entités dans cette maille distingue les réseaux cubique simple et cubique à faces centrées.
La structure microscopique du cristal conditionne certaines de ses propriétés macroscopiques, dont sa masse volumique.
Savoir-faire
Pour chacun des deux réseaux (cubique simple et cubique à faces centrées) : - représenter la maille en perspective cavalière ;
- calculer la compacité dans le cas d'entités chimiques sphériques tangentes ;
Savoirs
Un composé de formule chimique donnée peut cristalliser sous différents types de structures qui ont des propriétés macroscopiques différentes. Ainsi les minéraux se caractérisent par leur composition chimique et leur organisation cristalline. Une roche est formée de l'association de cristaux d'un même minéral ou de plusieurs minéraux.Des structures cristallines existent aussi dans les organismes biologiques (coquille, squelette, calcul rénal, etc.).
Savoir-faire
Distinguer, en termes d'échelle et d'organisation spatiale, maille, cristal, minéral, roche.Les identifier sur un échantillon ou une image.
Savoirs
Dans le cas des solides amorphes, l'empilement d'entités se fait sans ordre géométrique. C'est le cas du verre. Certaines roches volcaniques contiennent du verre, issu de la solidification très rapide d'une lave.Savoir-faire
Mettre en relation la structure amorphe ou cristalline d'une roche et les conditions de son refroidissement.Prérequis et limites
Les notions, déjà connues, d'entité chimique, de roche et de minéral sont remobilisées. L'objectif est de présenter l'organisation de la matière propre à l'état cristallin à partir d'exemples. La diversité des systèmes cristallins et des minéraux est seulement évoquée. La description de l'état cristallin est l'occasion d'utiliser les mathématiques (géométrie du cube et de la sphère, calculs de volumes, proportions) pour décrire la nature et quantifier ses propriétés.3. Une structure complexe : la cellule vivante
Dans le monde, la matière s'organise en structure d'ordre supérieur à l'échelle moléculaire. Un exemple est ici proposé : la structure cellulaire.
Savoirs
La découverte de l'unité cellulaire est liée à l'invention du microscope.L'observation de structures semblables dans de très nombreux organismes a conduit à énoncer le concept général de cellule et à construire la théorie cellulaire.
Plus récemment, l'invention du microscope électronique a permis l'exploration de l'intérieur de la cellule et la compréhension du lien entre échelle moléculaire et cellulaire.
Savoir-faire
Analyser et interpréter des documents historiques relatifs à la théorie cellulaire. Situer les ordres de grandeur : atome, molécule, organite, cellule, organisme.Savoirs
La cellule est un espace séparé de l'extérieur par une membrane plasmique. Cette membrane est constituée d'une bicouche lipidique et de protéines. La structure membranaire est stabilisée par le caractère hydrophile ou lipophile de certaines parties des molécules constitutives.Savoir-faire
Relier l'échelle de la cellule et celle de la molécule (exemple de la membrane plasmique).Schématiser la membrane plasmique à partir
de molécules dont les parties hydrophile/lipophile sont identifiées.
II. Le Soleil, notre source d'énergie
La Terre reçoit l'essentiel de son énergie du Soleil. Cette énergie conditionne la température de surface de la Terre et détermine climats et saisons. Elle permet la photosynthèse des végétaux et se transmet par la nutrition à d'autres êtres vivants.
Histoire, enjeux, débats
Repères historiques sur l'étude du rayonnement thermique (Stefan, Boltzmann, Planck, Einstein).Le discours sur l'énergie dans la société : analyse critique du vocabulaire d'usage courant (énergie fossile, énergie renouvelable, etc.).
L'albédo terrestre : un paramètre climatique majeur.
Distinction météorologie/climatologie.
1. Le rayonnement solaire
Le soleil transmet à la Terre de l'énergie par rayonnement.
Savoirs
L'énergie dégagée par les réactions de fusion de l'hydrogène qui se produisent dans les étoiles les maintient à une température très élevée.Du fait de l'équivalence masse-énergie (relation d'Einstein), ces réactions s'accompagnent d'une diminution de la masse solaire au cours du temps.
Comme tous les corps matériels, les étoiles et le Soleil émettent des ondes électromagnétiques et donc perdent de l'énergie par rayonnement.
Le spectre du rayonnement émis par la surface (modélisé par un spectre de corps noir) dépend seulement de la température de surface de l'étoile.
La longueur d'onde d'émission maximale est inversement proportionnelle à la température absolue de la surface de l'étoile (loi de Wien).
Savoir-faire
Déterminer la masse solaire transformée chaque seconde en énergie à partir de la donnée de la puissance rayonnée par le Soleil.À partir d'une représentation graphique du spectre d'émission du corps noir à une température donnée, déterminer la longueur d'onde d'émission maximale. Appliquer la loi de Wien pour déterminer la température de surface d'une étoile à partir de la longueur d'onde d'émission maximale.
Savoirs
La puissance radiative reçue du Soleil par une surface plane est proportionnelle à l'aire de la surface et dépend de l'angle entre la normale à la surface et la direction du Soleil.De ce fait, la puissance solaire reçue par unité de surface terrestre dépend :
- de l'heure (variation diurne) ;
- du moment de l'année (variation saisonnière) ;
- de la latitude (zonation climatique).
Savoir-faire
Sur un schéma, identifier les configurations pour lesquelles la puissance reçue par une surface est maximale ou minimale.Analyser, interpréter et représenter graphiquement des données de températures. Calculer des moyennes temporelles de températures. Comparer
des distributions temporelles de températures
Prérequis et limites
Les notions de base concernant l'énergie et la puissance, déjà connues, sont remobilisées. La loi de Planck n'est pas explicitée : toutes les analyses spectrales sont réalisées à partir de représentations graphiques.La relation entre la température absolue, exprimée en kelvin, et la température en degrés Celsius est fournie, ainsi que la loi de Wien.
2. Le bilan radiatif terrestre
La Terre reçoit le rayonnement solaire et émet elle-même un rayonnement. Le bilan conditionne le milieu de vie. La compréhension de cet équilibre en classe de première permettra d'aborder sa perturbation par l'humanité en terminale.
Savoirs
La proportion de la puissance totale, émise par le Soleil et atteignant la Terre, est déterminée par son rayon et sa distance au Soleil.Une fraction de cette puissance, quantifiée par l'albédo terrestre moyen, est diffusée par la Terre vers l'espace, le reste est absorbé par l'atmosphère, les continents et les océans.
Savoir-faire
En s'appuyant sur un schéma, calculer la proportion de la puissance émise par le Soleil qui atteint la Terre.L'albédo terrestre étant donné, déterminer la puissance totale reçue par le sol de la part du Soleil.
Savoirs
Le sol émet un rayonnement électromagnétique dans le domaine infra-rouge (longueur d'onde voisine de 10 μm) dont la puissance par unité de surface augmente avec la température.Une partie de cette puissance est absorbée par l'atmosphère, qui elle-même émet un rayonnement infrarouge vers le sol et vers l'espace (effet de serre).
La puissance reçue par le sol en un lieu donné est égale à la somme de la puissance reçue du Soleil et de celle reçue de l'atmosphère. Ces deux dernières sont du même ordre de grandeur.
Un équilibre, qualifié de dynamique, est atteint lorsque le sol reçoit au total une puissance moyenne égale à celle qu'il émet. La température moyenne du sol est alors constante.
Savoir-faire
Commenter la courbe d'absorption de l'atmosphère terrestre en fonction de la longueur d'ondeReprésenter sur un schéma les différents rayonnements reçus et émis par le sol. Expliquer qualitativement l'influence des différents facteurs (albedo, effet de serre) sur la température terrestre moyenne.
Prérequis et limites
Les notions de longueur d'onde du rayonnement et de spectre visible, déjà connues, sont remobilisées.L'objectif de ce paragraphe est de comprendre qualitativement comment le bilan énergétique de la Terre conditionne sa température.
La théorie de l'effet de serre et la connaissance de la loi de Stefan-Boltzmann ne sont pas exigibles.
Le réchauffement climatique global associé au renforcement de l'effet de serre sera étudié en détail en terminale, mais il peut être utilement mentionné.
3. Une conversion biologique de l'énergie solaire : la photosynthèse
L'utilisation par la photosynthèse d'une infime partie de l'énergie solaire reçue par la planète fournit l'énergie nécessaire à l'ensemble des êtres vivants (à l'exception de certains milieux très spécifiques non évoqués dans ce programme).
Savoirs
Une partie du rayonnement solaire absorbé par les organismes chlorophylliens permet la synthèse de matière organique à partir d'eau, de sels minéraux et de dioxyde de carbone (photosynthèse). À l'échelle de la planète, les organismes chlorophylliens utilisent pour la photosynthèse environ 0,1 % de la puissance solaire totale disponible. À l'échelle de la feuille (pour les plantes), la photosynthèse utilise une très faible fraction de la puissance radiative reçue, le reste est soit diffusé, soit transmis, soit absorbé (échauffement et évapotranspiration).La photosynthèse permet l'entrée dans la biosphère de matière minérale stockant de l'énergie sous forme chimique.
Ces molécules peuvent être transformées par respiration ou fermentation pour libérer l'énergie nécessaire au fonctionnement des êtres vivants.
Savoir-faire
Recenser, extraire et organiser des informations pour prendre conscience de l'importance planétaire de la photosynthèse.Comparer les spectres d'absorption et d'action photosynthétique d'un végétal.
Représenter sur un schéma les différents échanges d'énergie au niveau d'une feuille.
Savoirs
À l'échelle des temps géologiques, une partie de la matière organique s'accumule dans les sédiments puis se transforme en donnant des combustibles fossiles : gaz, charbon, pétrole.Savoir-faire
À partir de l'étude d'un combustible fossile ou d'une roche de son environnement, discuter son origine biologique.Prérequis et limites
Les notions de biologie et géologie utiles à ce paragraphe, déjà connues, sont remobilisées (photosynthèse, respiration, fermentation, sédimentation, combustible fossile). Sans les approfondir, il s'agit de montrer comment elles sont utiles pour comprendre les flux d'énergie à différentes échelles.Aucun développement sur les mécanismes cellulaires et moléculaires n'est exigible.
4. Le bilan thermique du corps humain
La température du corps est stable. Cette stabilité résulte d'un ensemble de flux présentés ici.
Savoirs
La température du corps reste stable parce que l'énergie qu'il libère est compensée par l'énergie dégagée par la respiration cellulaire ou les fermentations.Globalement, la puissance thermique libérée par un corps humain dans les conditions de vie courante, au repos, est de l'ordre de 100 W.
Savoir-faire
Représenter sur un schéma qualitatif les différents échanges d'énergie entre l'organisme et le milieu extérieur. Utiliser des données quantitatives sur l'apport énergétique d'aliments dans un bilan d'énergie correspondant à des activités variées.Prérequis et limites
Les notions de conservation et de conversion d'énergie, déjà connues, sont remobilisées. La respiration et le rôle énergétique des aliments, déjà connus, sont remobilisés.Aucun développement n'est attendu concernant les mécanismes cellulaires et moléculaires.
III. La Terre, un astre singulier
La Terre, singulière parmi un nombre gigantesque de planètes, est un objet d'étude ancien. Les évidences apparentes et les récits non scientifiques ont d'abord conduit à de premières représentations. La compréhension scientifique de sa forme, son âge et son mouvement résulte d'un long cheminement, émaillé de controverses.
Histoire, enjeux et débats
L'histoire de la mesure du méridien terrestre par Ératosthène (et les hypothèses d'Anaxagore). L'histoire de la mesure du méridien terrestre par Delambre et Méchain (détermination de la longueur du méridien reliant Dunkerque à Barcelone). Histoire de la définition du mètre.Quelques grandes étapes de l'étude de l'âge de la Terre : Buffon, Darwin, Kelvin, Rutherford. Modalités de la construction d'une approche scientifique d'une question controversée pour aboutir à un résultat stabilisé.
Grandes étapes de la controverse sur l'organisation du système solaire : Ptolémée, Copernic, Galilée, Kepler, Tycho Brahe, Newton.
1. La forme de la Terre
L'environnement « plat » à notre échelle de perception cache la forme réelle de la Terre, dont la compréhension résulte d'une longue réflexion. Au-delà de la dimension historique et culturelle, la mise en œuvre de différentes méthodes de calcul de longueurs à la surface de la Terre permet de développer des compétences mathématiques de calcul et de représentation et invite à exercer un esprit critique sur les différents résultats obtenus, les approximations réalisées et les limites d'un modèle.
Savoirs
Dès l'Antiquité, des observations de différentes natures ont permis de conclure que la Terre était sphérique, alors même que, localement, elle apparaît plane dans la plupart des expériences quotidiennes.Historiquement, des méthodes géométriques ont permis de calculer la longueur d'un méridien (environ 40 000 km) à partir de mesures d'angles ou de longueurs :
méthodes d'Ératosthène et de triangulation plane.
Savoir-faire
Calculer la longueur du méridien terrestre par la méthode d'Ératosthène.Calculer une longueur par la méthode de triangulation utilisée par Delambre et Méchain.
Calculer le rayon de la Terre à partir de la longueur du méridien.
Savoirs
On repère un point à la surface de la Terre par deux coordonnées angulaires, sa latitude et sa longitude.Le plus court chemin entre deux points à la surface de la Terre est l'arc du grand cercle qui les relie.
Savoir-faire
Calculer la longueur d'un arc de méridien et d'un arc de parallèle.Comparer, à l'aide d'un système d'information géographique, les longueurs de différents chemins reliant deux points à la surface de la Terre.
Prérequis et limites
La connaissance de la loi des sinus (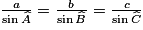 ) n'est pas exigible. Elle est fournie pour mettre en œuvre le principe de triangulation plane (calcul d'une longueur à partir de la mesure d'une autre longueur et de deux angles).
) n'est pas exigible. Elle est fournie pour mettre en œuvre le principe de triangulation plane (calcul d'une longueur à partir de la mesure d'une autre longueur et de deux angles).On admet que la longueur d'un arc de cercle est proportionnelle à l'angle qui l'intercepte. Le repérage sur une sphère, déjà connu des élèves, est remobilisé.
Le calcul de la longueur entre deux points le long d'un grand cercle n'est pas exigible.
2. L'histoire de l'âge de la Terre
L'âge de la Terre est d'un ordre de grandeur sans rapport avec la vie humaine. Sa compréhension progressive met en œuvre des arguments variés.
Savoirs
Au cours de l'histoire des sciences, plusieurs arguments ont été utilisés pour aboutir à la connaissance actuelle de l'âge de la Terre :temps de refroidissement, empilements sédimentaires, évolution biologique, radioactivité.
L'âge de la Terre aujourd'hui précisément déterminé est de 4,57.109 ans.
Savoir-faire
Interpréter des documents présentant des arguments historiques utilisés pour comprendre l'âge de la Terre.Identifier diverses théories impliquées dans la controverse scientifique de l'âge de la Terre.
Prérequis et limites
L'objectif n'est pas de connaître dans le détail les arguments utilisés au cours de l'histoire des sciences, mais de savoir interpréter des données relatives à ces arguments. Il s'agit de prendre appui sur cet exemple pour montrer comment la science construit et perfectionne peu à peu sa compréhension de la nature, en exploitant des faits nouveaux apparus successivement. Il s'agit aussi de montrer qu'une question scientifique complexe est résolue grâce à la participation de plusieurs domaines de spécialité.3. La Terre dans l'Univers
Le mouvement de la Terre dans l'Univers a été l'objet de célèbres et violentes controverses.
L'étude de quelques aspects de ces débats permet de comprendre la difficulté de la construction du savoir scientifique.
L'étude de quelques aspects de ces débats permet de comprendre la difficulté de la construction du savoir scientifique.
Savoirs
Observée dans un référentiel fixe par rapport aux étoiles, la Terre parcourt une trajectoire quasi circulaire autour du Soleil.Le passage d'une conception géocentrique à une conception héliocentrique constitue l'une des controverses majeures de l'histoire des sciences.
Savoir-faire
Interpréter des documents présentant des arguments historiques pour discuter la théorie héliocentrique.Savoirs
Observée dans un référentiel géocentrique, la Lune tourne autour de la Terre sur une trajectoire quasi-circulaire. Elle présente un aspect qui varie au cours de cette rotation (phases).La Lune tourne également sur elle-même et présente toujours la même face à la Terre.
Savoir-faire
Interpréter l'aspect de la Lune dans le ciel en fonction de sa position par rapport à la Terre et au Soleil.Prérequis et limites
L'organisation du système solaire est déjà connue. L'accent est mis ici sur la compréhension de cette organisation au cours de l'histoire des sciences et sur l'importance des controverses scientifiques concernées.IV. Son et musique, porteurs d'information
L'être humain perçoit le monde à l'aide de signaux dont certains sont de nature sonore. De l'Antiquité jusqu'à nos jours, il a combiné les sons de manière harmonieuse pour en faire un art, la musique, qui entretient des liens privilégiés avec les mathématiques. L'informatique permet aujourd'hui de numériser les sons et la musique.
La compréhension des mécanismes auditifs s'inscrit dans une perspective d'éducation à la santé.
La compréhension des mécanismes auditifs s'inscrit dans une perspective d'éducation à la santé.
Histoire, enjeux, débats
L'histoire de l'analyse temps-fréquence depuis Fourier.La controverse entre d'Alembert, Euler et Daniel Bernoulli sur le problème des cordes vibrantes.
L'histoire des gammes, de Pythagore à Bach.
Des algorithmes au cœur de la composition musicale : de l'Offrande musicale de Bach à la musique contemporaine.
Les enjeux culturels et économiques de la numérisation et de la compression des sons. La santé auditive.
1. Le son, phénomène vibratoire
La banalité du son dans l'environnement cache une réalité physique précise.
Savoirs
Un son pur est associé à un signal dépendant du temps de façon sinusoïdale.Un signal périodique de fréquence f se décompose en une somme de signaux sinusoïdaux de fréquences multiples de f. Le son associé à ce signal est un son composé. f est appelée fréquence fondamentale, les autres fréquences sont appelées harmoniques.
La puissance par unité de surface transportée par une onde sonore est quantifiée par son intensité. Son niveau d'intensité sonore est exprimé en décibels selon une échelle logarithmique.
Savoir-faire
Utiliser un logiciel permettant de visualiser le spectre d'un son. Utiliser un logiciel pour produire des sons purs et composés.Relier puissance sonore par unité de surface et niveau d'intensité sonore exprimé en décibels.
Savoirs
Une corde tendue émet en vibrant un son composé dont la fréquence fondamentale ne dépend que de ses caractéristiques (longueur, tension, masse linéique).Dans les instruments à vent, un phénomène analogue se produit par vibration de l'air dans un tuyau.
Savoir-faire
Relier qualitativement la fréquence fondamentale du signal émis et la longueur d'une corde vibrante.Prérequis et limites
Les notions de son et de fréquence, déjà connues des élèves, sont remobilisées. La sinusoïde est définie à partir de sa représentation graphique. Aucune construction mathématique de la fonction n'est attendue.La formule donnant la fréquence fondamentale d'une corde vibrante en fonction de ses caractéristiques n'est pas exigible.
2. La musique ou l'art de faire entendre les nombres
Comment l'analyse mathématique du phénomène vibratoire du son aboutit-elle à une production artistique ?
La musique et les mathématiques sont deux langages universels. Les Grecs anciens les ont dotés d'une origine commune puisque la théorie pythagoricienne des proportions avait pour but de percer les secrets de l'harmonie musicale. Depuis, les évolutions de la musique et des mathématiques se sont enrichies mutuellement.
La musique et les mathématiques sont deux langages universels. Les Grecs anciens les ont dotés d'une origine commune puisque la théorie pythagoricienne des proportions avait pour but de percer les secrets de l'harmonie musicale. Depuis, les évolutions de la musique et des mathématiques se sont enrichies mutuellement.
Savoirs
En musique, un intervalle entre deux sons est défini par le rapport (et non la différence) de leurs fréquences fondamentales.Deux sons dont les fréquences sont dans le rapport 2/1 correspondent à une même note, à deux hauteurs différentes. L'intervalle qui les sépare s'appelle une octave.
Savoirs
Une gamme est une suite finie de notes réparties sur une octave.Dans l'Antiquité, la construction des gammes était basée sur des fractions simples, (2/1, 3/2, 4/3, etc.). En effet, des sons dont les fréquences sont dans ces rapports simples étaient alors considérés comme les seuls à être consonants.
Une quinte est un intervalle entre deux fréquences de rapport 3/2.
Les gammes dites de Pythagore sont basées sur le cycle des quintes.
Pour des raisons mathématiques, ce cycle des quintes ne « reboucle » jamais sur la note de départ. Cependant, les cycles de 5, 7 ou 12 quintes « rebouclent » presque. Pour les gammes associées, l'identification de la dernière note avec la première impose que l'une des quintes du cycle ne corresponde pas exactement à la fréquence 3/2.
Savoir-faire
Calculer des puissances et des quotients en lien avec le cycle des quintes.Mettre en place un raisonnement mathématique pour prouver que le cycle des quintes est infini.
Savoirs
Les intervalles entre deux notes consécutives des gammes dites de Pythagore ne sont pas égaux, ce qui entrave la transposition.La connaissance des nombres irrationnels a permis, au xviie siècle, de construire des gammes à intervalles égaux.
Savoir-faire
Utiliser la racine douzième de 2 pour partager l'octave en douze intervalles égaux.Prérequis et limites
La construction des gammes dites de Pythagore s'appuie sur des connaissances mathématiques acquises au collège sur les fractions et les puissances et permet de les mobiliser dans un contexte artistique. L'introduction des gammes « au tempérament égal » permet de comprendre en quoi la découverte des nombres irrationnels a des applications en dehors du champ mathématique.La racine douzième de 2 est introduite par analogie avec la racine carrée, en lien avec l'utilisation de la calculatrice.
3. Le son, une information à coder
Le son, vibration de l'air, peut être enregistré sur un support informatique. Les techniques numériques ont mis en évidence un nouveau type de relations entre les sciences et les sons, le processus de numérisation dérivant lui-même de théories mathématiques et informatiques.
Savoirs
Pour numériser un son, on procède à la discrétisation du signal analogique sonore (échantillonnage et quantification).Plus la fréquence d'échantillonnage est élevée et la quantification est fine, plus la numérisation est fidèle, mais plus la taille du fichier audio est grande. La reproduction fidèle du signal analogique nécessite une fréquence d'échantillonnage au moins double de celle du son.
Savoir-faire
Justifier le choix des paramètres de numérisation d'un son.Estimer la taille d'un fichier audio.
Savoirs
La compression consiste à diminuer la taille d'unfichier afin de faciliter son stockage et sa transmission.
Les techniques de compression spécifiques au son, dites « avec perte d'information », éliminent les informations sonores auxquelles l'oreille est peu sensible.
Savoir-faire
Calculer un taux de compression.Comparer des caractéristiques et des qualités de fichiers audio compressés.
Prérequis et limites
L'étude de la numérisation du son s'appuie sur les connaissances acquises dans l'enseignement « Sciences numériques et technologie » de seconde en matière de numérisation d'images.4. Entendre la musique
L'air qui vibre n'est musique que parce que notre oreille l'entend et que notre cerveau la perçoit comme telle. Mais l'excès de sons, même s'il est musical, est une forme de perturbation de l'environnement.
Savoirs
L'oreille externe canalise les sons du milieu extérieur vers le tympan. Cette membrane vibrante transmet ces vibrations jusqu'à l'oreille interne par l'intermédiaire de l'oreille moyenne.Savoir-faire
Relier l'organisation de l'oreille externe et de l'oreille moyenne à la réception et la transmission de la vibration sonore.Savoirs
L'être humain peut percevoir des sons de niveaux d'intensité approximativement compris entre 0 et 120 dB.Les sons audibles par les humains ont des fréquences comprises entre 20 000 et 20 000 Hz. Dans l'oreille interne, des structures cellulaires (cils vibratiles) entrent en résonance avec les vibrations reçues et les traduisent en un message nerveux qui se dirige vers le cerveau.
Les cils vibratiles sont fragiles et facilement endommagés par des sons trop intenses. Les dégâts sont alors irréversibles et peuvent causer une surdité.
Savoir-faire
Relier la structure des cellules ciliées à la perception du son et à la fragilité du système auditif.Relier l'intensité du son au risque encouru par l'oreille interne.
Savoirs
Des aires cérébrales spécialisées reçoivent les messages nerveux auditifs. Certaines permettent, après apprentissage, l'interprétation de l'univers sonore (parole, voix, musique, etc.).Savoir-faire
Interpréter des données d'imagerie cérébrale relatives au traitement de l'information sonore.Prérequis et limites
La connaissance approfondie de la physiologie de l'audition n'est pas l'objectif duprogramme. En particulier, les modalités de transduction de la vibration auditive en message nerveux ne sont pas exigibles. Il s'agit simplement de présenter dans ses grandes lignes le passage du phénomène physique du son à la sensibilité auditive consciente, en faisant apparaître les rôles respectifs de l'oreille et du cerveau.
5. Projet expérimental et numérique
Le projet s'articule autour de la mesure et des données qu'elle produit, qui sont au cœur des sciences expérimentales. L'objectif est de confronter les élèves à la pratique d'une démarche scientifique expérimentale, de l'utilisation de matériels (capteurs et logiciels) à l'analyse critique des résultats.
Le projet expérimental et numérique comporte trois dimensions :
La dimension numérique repose sur l'utilisation de matériels (capteur éventuellement associé à un microcontrôleur) et de logiciels (tableur, environnement de programmation).
Le projet expérimental et numérique comporte trois dimensions :
- utilisation d'un capteur éventuellement réalisé en classe ;
- acquisition numérique de données ;
- traitement mathématique, représentation et interprétation de ces données.
La dimension numérique repose sur l'utilisation de matériels (capteur éventuellement associé à un microcontrôleur) et de logiciels (tableur, environnement de programmation).
Prérequis et limites
Ce projet remobilise certains acquis des classes antérieures : mesure et incertitudes, manipulation de capteurs et microcontrôleurs, données structurées et leur traitement, information chiffrée et statistique descriptive, utilisation d'un tableur et d'un environnement de programmation. L'objectif n'est pas d'introduire des notions nouvelles.V. Nouveau programme de mathématiques intégré à l'enseignement scientifique
Le programme est structuré autour de trois parties thématiques :
- analyse de l'information chiffrée (statistiques) ;
- phénomènes aléatoires (probabilités conditionnelles) ;
- phénomènes d'évolution (analyse : suites, fonctions, exponentielles, dérivée) ;
- automatismes (lecture et production de graphiques, traitement de données, calcul numérique et algébrique).
Les trois parties thématiques sont organisées selon deux colonnes : « Situations et problèmes » et « Contenus mathématiques ». Seuls sont exigibles des élèves les contenus mathématiques de la colonne de droite, mobilisés dans les capacités attendues.
Le programme repose sur des mises en situation et des problèmes issus des disciplines enseignées au lycée, mais aussi de la vie quotidienne ou de la vie citoyenne, qui peuvent, selon le choix de l'enseignant, motiver l'introduction des notions étudiées ou les illustrer. Le professeur a la possibilité de choisir d'autres situations que celles proposées dans la colonne de gauche.
Selon les projets et les centres d'intérêt des élèves, il est possible de proposer des rapprochements avec d'autres disciplines qui ne sont pas mentionnées dans ce programme (littérature, arts plastiques, etc.)
Le programme repose sur des mises en situation et des problèmes issus des disciplines enseignées au lycée, mais aussi de la vie quotidienne ou de la vie citoyenne, qui peuvent, selon le choix de l'enseignant, motiver l'introduction des notions étudiées ou les illustrer. Le professeur a la possibilité de choisir d'autres situations que celles proposées dans la colonne de gauche.
Selon les projets et les centres d'intérêt des élèves, il est possible de proposer des rapprochements avec d'autres disciplines qui ne sont pas mentionnées dans ce programme (littérature, arts plastiques, etc.)
1. Analyse de l'information chiffrée
L'analyse de l'information chiffrée portant sur des problématiques d'actualité (développement durable, changement climatique, biodiversité, économie, démographie, santé publique, etc.) permet d'éclairer les élèves sur certains débats actuels et de développer le sens critique.
En prolongement du programme de seconde dans lequel ont été introduits des indicateurs utiles pour l'analyse d'un unique caractère statistique, cette partie aborde l'analyse statistique bivariée. Il s'agit d'une première sensibilisation aux bases de données.
Certaines données étudiées peuvent être issues de ressources d'autres enseignement dispensés au lycée (enseignement scientifique, enseignement moral et civique, enseignement de spécialité). Les possibilités offertes par l'informatique permettent le stockage et la manipulation de données massives. Certaines de ces données sont disponibles sur des sites institutionnels comme ceux de l'Institut national de la statistique et des études économiques (Insee), de l'Institut national d'études démographiques (Ined) ou dans le catalogue data.gouv des données de l'administration. D'autres figurent dans des rapports publics comme ceux du Groupe d'experts intergouvernemental sur l'évolution du climat (Giec).
L'analyse bivariée cherche à étudier les éventuelles relations entre deux caractères. Elle doit s'illustrer en utilisant des représentations de données réelles, qui peuvent aussi s'obtenir par le traitement à l'aide d'un tableur de fichiers d'une taille raisonnable.
En prolongement du programme de seconde dans lequel ont été introduits des indicateurs utiles pour l'analyse d'un unique caractère statistique, cette partie aborde l'analyse statistique bivariée. Il s'agit d'une première sensibilisation aux bases de données.
Certaines données étudiées peuvent être issues de ressources d'autres enseignement dispensés au lycée (enseignement scientifique, enseignement moral et civique, enseignement de spécialité). Les possibilités offertes par l'informatique permettent le stockage et la manipulation de données massives. Certaines de ces données sont disponibles sur des sites institutionnels comme ceux de l'Institut national de la statistique et des études économiques (Insee), de l'Institut national d'études démographiques (Ined) ou dans le catalogue data.gouv des données de l'administration. D'autres figurent dans des rapports publics comme ceux du Groupe d'experts intergouvernemental sur l'évolution du climat (Giec).
L'analyse bivariée cherche à étudier les éventuelles relations entre deux caractères. Elle doit s'illustrer en utilisant des représentations de données réelles, qui peuvent aussi s'obtenir par le traitement à l'aide d'un tableur de fichiers d'une taille raisonnable.
| Situations et problèmes | Contenus mathématiques |
|---|---|
| Analyse croisée de couples de caractères (exemples : genre, âge, revenus, indicateurs de santé, indicateurs financiers, température, niveau des océans, proportion de gaz à effet de serre, etc.). Les données peuvent être présentées sous la forme d'un tableau ou d'un diagramme obtenu à partir d'un fichier de données en utilisant un tableur. | Analyse statistique de deux caractères. Tableau croisé d'effectifs. Exemples d'analyse du croisement de deux caractères par représentation graphique (nuage de points, diagrammes en barres, diagrammes circulaires). Détermination dans un fichier de données d'un sous-ensemble d'individus répondant à un sous-caractère (filtre, utilisation des ET, OU, NON). |
Capacités attendues
- Dresser un tableau croisé de deux caractères à partir d'un fichier de données.
- Utiliser un tableur pour représenter des données sous forme de tableau ou de diagramme.
2. Phénomènes aléatoires
L'analyse statistique bivariée abordée dans la partie précédente permet d'introduire naturellement la notion de fréquence conditionnelle. Dans le cas d'un tirage aléatoire dans une population finie, la fréquence peut être identifiée à une probabilité.
La notion de probabilité conditionnelle permet d'introduire de manière intuitive celle de l'indépendance : deux événements A et B sont dits indépendants si la probabilité conditionnelle de A sachant B est égale à la probabilité de A (sous réserve de la non-nullité de celle de B).
Grâce à des outils numériques, on simule une succession de tirages aléatoires indépendants (par exemple, des tirages avec remise dans une urne) afin de poursuivre l'approche vulgarisée de la loi des grands nombres initiée en classe de seconde.
La possibilité de présenter des problèmes simples relatifs à des jeux de hasard datant du XVIIIe siècle confère à cette partie une dimension historique.
La notion de probabilité conditionnelle permet d'introduire de manière intuitive celle de l'indépendance : deux événements A et B sont dits indépendants si la probabilité conditionnelle de A sachant B est égale à la probabilité de A (sous réserve de la non-nullité de celle de B).
Grâce à des outils numériques, on simule une succession de tirages aléatoires indépendants (par exemple, des tirages avec remise dans une urne) afin de poursuivre l'approche vulgarisée de la loi des grands nombres initiée en classe de seconde.
La possibilité de présenter des problèmes simples relatifs à des jeux de hasard datant du XVIIIe siècle confère à cette partie une dimension historique.
| Situations et problèmes | Contenus mathématiques |
|---|---|
| Sciences de la vie Tests médicaux : faux positifs et faux négatifs. Théorie des jeux Modélisation ou simulation de jeux simples : pile ou face, jeu de « croix ou pile » de d'Alembert, jeu de pierre-feuille-ciseaux, jeu du lièvre et de la tortue, jeu du « passe-dix » (problème du grand-duc de Toscane). Stratégie gagnante au jeu de Monty Hall. Histoire des mathématiques Traduction en langage des probabilités de la correspondance épistolaire entre Fermat et Pascal à propos du problème des partis. | Fréquence conditionnelle, fréquence marginale. Probabilité conditionnelle : définition, notation, calcul à partir d'un tableau croisé d'effectifs ou d'un arbre de probabilités. Indépendance de deux événements. Succession d'événements indépendants, équiprobables ou non. |
Capacités attendues
- Construire un tableau croisé d'effectifs ou un arbre de probabilité associé à un phénomène aléatoire.
- Calculer des fréquences conditionnelles et des fréquences marginales à partir d'un tableau croisé d'effectifs.
- Interpréter un tableau croisé en utilisant des fréquences conditionnelles.
- Calculer des probabilités conditionnelles à l'aide d'un tableau croisé d'effectifs ou d'un arbre pondéré.
3. Phénomènes d'évolution
Cette partie est consacrée à des notions mathématiques permettant de modéliser des phénomènes en évolution : les suites, qui modélisent des grandeurs dont l'évolution est discrète, et les fonctions, qui modélisent des grandeurs dont l'évolution est continue.
L'objectif est d'appréhender deux modèles classiques d'évolution, la croissance linéaire et la croissance exponentielle, sans exclure la présentation d'autres modèles.
La compréhension et l'interrogation critique des modèles étudiés permettent de développer des capacités de raisonnement et d'argumentation. Leur mise en pratique, tant dans des situations internes qu'externes aux mathématiques, permet de consolider des habiletés en matière de calcul, d'analyse et de production de graphiques ainsi que dans l'utilisation d'outils numériques.
Les deux modes de génération d'une suite, par récurrence et explicite, peuvent être introduits lors de la résolution de problèmes. On peut, par exemple, prendre appui sur des motifs géométriques ou sur un contexte historique, comme le problème de remboursement d'une dette posé par Euler dans Introduction à l'analyse infinitésimale.
Lors des premières modélisations d'une grandeur discrète par une suite, on veille à utiliser la notation fonctionnelle u(n), préalablement à la notation indicielle un.
L'objectif est d'appréhender deux modèles classiques d'évolution, la croissance linéaire et la croissance exponentielle, sans exclure la présentation d'autres modèles.
La compréhension et l'interrogation critique des modèles étudiés permettent de développer des capacités de raisonnement et d'argumentation. Leur mise en pratique, tant dans des situations internes qu'externes aux mathématiques, permet de consolider des habiletés en matière de calcul, d'analyse et de production de graphiques ainsi que dans l'utilisation d'outils numériques.
Les deux modes de génération d'une suite, par récurrence et explicite, peuvent être introduits lors de la résolution de problèmes. On peut, par exemple, prendre appui sur des motifs géométriques ou sur un contexte historique, comme le problème de remboursement d'une dette posé par Euler dans Introduction à l'analyse infinitésimale.
Lors des premières modélisations d'une grandeur discrète par une suite, on veille à utiliser la notation fonctionnelle u(n), préalablement à la notation indicielle un.
Croissance linéaire
Les suites arithmétiques et les fonctions affines modélisent des grandeurs discrètes ou continues dont le taux d'accroissement est constant. Les fonctions affines, déjà étudiées en classe de seconde, peuvent faire l'objet d'un travail succinct. Le professeur peut mettre en parallèle le sens de variation des fonctions affines et celui des suites arithmétiques.| Situations et problèmes | Contenus mathématiques |
|---|---|
| Éducation économique, financière et budgétaire Placement à intérêts simples, croissance d'un poste budgétaire. Dénombrement Motifs géométriques évolutifs en forme de T ou de croix, carré bordé. | Suites arithmétiques Définition par la relation de récurrence. Explicitation du terme de rang n. Sens de variation. Représentation graphique. |
| Physique Correspondance entre degrés Celsius et Fahrenheit. Économie Modélisation de l'offre et de la demande par des fonctions affines, point d'équilibre. Enseignement moral et civique Modélisation du barème de l'impôt sur le revenu par une fonction affine par morceaux (taux marginal, taux moyen). Sciences de la Terre Modèle linéaire de l'évolution du niveau moyen des océans. | Fonctions affines L'objectif est de remobiliser les connaissances abordées en classe de seconde : représentation graphique, sens de variation, lien entre le taux d'accroissement et le coefficient directeur de la droite représentative. |
Capacités attendues
- Reconnaître un phénomène discret ou continu de croissance linéaire et savoir le modéliser.
- Calculer un terme de rang donné d'une suite arithmétique définie par une relation fonctionnelle ou une relation de récurrence.
- Réaliser et exploiter la représentation graphique des termes d'une suite arithmétique ou d'une fonction affine.
- Résoudre un problème de seuil dans le cas d'une croissance linéaire.
Croissance exponentielle
Les suites géométriques modélisent des grandeurs discrètes dont le taux d'évolution est constant.Les fonctions exponentielles sont présentées comme un prolongement des suites géométriques de raison positive à des valeurs non entières positives.
Dans le cadre d'une approche différenciée de cette introduction, il est possible :
- de se limiter au recours à la calculatrice pour obtenir la valeur de ax pour tout réel positif x ;
- de « compléter » le nuage de points représentant une suite géométrique pour obtenir la courbe d'une fonction continue ;
- d'ajouter des « points intermédiaires » à ce nuage par dichotomies successives (moyenne arithmétique des abscisses et moyenne géométrique des ordonnées) à l'aide d'un tableur ;
- de commencer par définir la racine n-ième d'un réel positif, puis de construire les puissances à exposant rationnel positif afin de conserver les propriétés des fonctions puissances entières étudiées en seconde.
Le professeur peut mettre en parallèle le sens de variation des fonctions exponentielles et celui des suites géométriques.
| Situations et problèmes | Contenus mathématiques |
|---|---|
| Sciences de la vie Élimination d'une substance dans le sang. Dénombrement Motifs géométriques évolutifs (triangle de Sierpinski, etc.). Éducation économique, financière et budgétaire Emprunt, placement à intérêts composés, gestion d'une dette, croissance d'un poste budgétaire. | Suites géométriques à termes strictement positifs Définition par relation de récurrence. Explicitation du terme de rang n. Sens de variation. Représentation graphique. |
| Éducation économique, financière et budgétaire Valeur au bout d'une fraction d'annuité d'un capital placé à intérêts composés à taux annuel constant. Économie, géographie Analyse comparée de l'accroissement d'une population et des ressources alimentaires (modèle de Malthus). Sciences sociales Modélisation simplifiée de la propagation d'une rumeur (cascades verticales). Physique et sciences de la vie et de la Terre Nombre de noyaux radioactifs présents dans un échantillon au bout d'une fraction de demi-vie. Applications à la médecine et à la datation par le carbone 14. Sciences de la vie Taux de reproduction 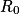 d'un virus lors d'une épidémie. d'un virus lors d'une épidémie. | Fonctions exponentielles Introduction de la fonction 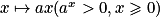 Propriétés algébriques (admises, par extension des propriétés des puissances entières). Variations. Représentation graphique. Cas particulier de l'exposant 1/n. Taux d'évolution moyen correspondant à n évolutions successives. |
Capacités attendues
- Reconnaître un phénomène discret ou continu de croissance exponentielle et savoir le modéliser.
- Calculer un terme de rang donné d'une suite géométrique définie par une relation fonctionnelle ou une relation de récurrence.
- Calculer un taux d'évolution moyen.
- Réaliser et exploiter la représentation graphique des termes d'une suite géométrique ou d'une fonction exponentielle.
- Résoudre un problème de seuil dans le cas d'une croissance exponentielle par le calcul, à l'aide d'une représentation graphique ou en utilisant un outil numérique.
Variation instantanée, variation globale
La notion de dérivée est utilisée pour étudier les variations de certains phénomènes.On met en évidence par des zooms successifs qu'une courbe donnée a localement l'apparence d'une droite. Après cette sensibilisation, le nombre dérivé peut être présenté, à l'aide d'un logiciel de géométrie dynamique, comme étant le coefficient directeur de la tangente, position limite des sécantes passant par le point considéré.
Dans le cadre de la différenciation, ce nombre peut aussi être introduit en considérant la vitesse instantanée d'un mobile à un instant donné.
L'approche graphique se prolonge globalement dans la découverte du lien entre le signe de la fonction dérivée et les variations de la fonction.
Parmi les outils mathématiques permettant de traiter des problèmes d'optimisation, l'un des plus simples et des plus efficaces est le signe de la fonction dérivée. Pour identifier un extremum, la seule analyse du tableau de variation suffit.
Dans le cas de fonctions donnant lieu à des calculs complexes, on peut recourir à un logiciel de calcul formel qui permet d'obtenir ou de factoriser la dérivée afin de résoudre le problème posé.
On peut s'appuyer sur des données réelles en utilisant un tableur pour modéliser leur évolution globale à l'aide d'une courbe de tendance polynomiale et étudier leurs variations.
| Situations et problèmes | Contenus mathématiques |
|---|---|
| Sciences de la vie Courbe de croissance d'un enfant. Physique Vitesse instantanée d'un mobile animé d'un mouvement rectiligne. Chimie Vitesse d'apparition d'un produit ou de disparition d'un réactif dans une réaction chimique. Économie Coût marginal défini comme la variation du coût total induite par la production et la vente d'une unité supplémentaire, et modélisé par la dérivée du coût total. | Variation instantanée (nombre dérivé) Tangente à une courbe en un point. Nombre dérivé comme coefficient directeur de la tangente. |
| Économie Modélisation par une fonction du coût de production et du chiffre d'affaires d'une entreprise, étude du bénéfice. Optimisation des dimensions d'un emballage pour en réduire le coût. | Variation globale (fonction dérivée) Fonction dérivée. Sens de variation d'une fonction, lien avec le signe de la fonction dérivée sur un intervalle. Dérivée des fonctions constante, identité, carré et cube. Dérivée d'une somme, du produit par un nombre réel. Application à la dérivée d'un polynôme de degré inférieur ou égal à 3. Tableau de variation, à l'aide si besoin d'un logiciel de calcul formel. |
Capacités attendues
- Interpréter le nombre dérivé dans le cadre d'un modèle d'évolution.
- Interpréter géométriquement le nombre dérivé comme coefficient directeur de la tangente.
- Décrire les variations d'un phénomène en mobilisant la dérivée d'une fonction.
- Déterminer le sens de variation d'une fonction polynomiale de degré inférieur ou égal à trois (la forme factorisée de la dérivée pourra être donnée).
- Prévoir l'évolution d'un phénomène grâce à l'étude de la dérivée d'une fonction.
4. Automatismes
Cette partie du programme vise à construire et à entretenir des habiletés mathématiques (connaissances, procédures et stratégies) dans les domaines des représentations graphiques, du traitement des données et du calcul. Il s'agit à la fois de garantir un socle de connaissances et de compétences fondamentales nécessaires à tout citoyen, d'asseoir des réflexes intellectuels pour s'engager avec succès dans la résolution de problèmes et pour développer une posture critique et réfléchie dans la lecture et la représentation de données.
Sans faire l'objet d'un chapitre d'enseignement spécifique, le développement des capacités énoncées ci-dessous requiert un entraînement régulier tout au long de l'année, par exemple lors d'activités ritualisées de début de séance sous forme de « questions flash », privilégiant l'activité mentale et la verbalisation des procédures.
Il convient de s'appuyer sur des situations simples pour ne pas occulter l'objectif d'apprentissage par des difficultés inhérentes à la compréhension de l'énoncé.
Sans faire l'objet d'un chapitre d'enseignement spécifique, le développement des capacités énoncées ci-dessous requiert un entraînement régulier tout au long de l'année, par exemple lors d'activités ritualisées de début de séance sous forme de « questions flash », privilégiant l'activité mentale et la verbalisation des procédures.
Il convient de s'appuyer sur des situations simples pour ne pas occulter l'objectif d'apprentissage par des difficultés inhérentes à la compréhension de l'énoncé.
Représentations graphiques
- Préciser sur un graphique les grandeurs en jeu, les unités et les échelles.
- Lire sur un graphique les variations d'une grandeur : croissance ou décroissance, doublement régulier, accélération ou ralentissement de la croissance.
- Estimer graphiquement une valeur atteinte, un antécédent, un seuil.
Traitement de données
Appliquer un pourcentage d'augmentation ou de diminution.
Calculer un taux d'évolution global à partir de taux d'évolution successifs, calculer un taux d'évolution réciproque.
Appliquer un pourcentage d'augmentation ou de diminution.
Calculer un taux d'évolution global à partir de taux d'évolution successifs, calculer un taux d'évolution réciproque.
Calcul numérique et algébrique
- Effectuer mentalement des calculs simples mettant en jeu des nombres décimaux, des fractions et des pourcentages.
- Passer d'une écriture d'un nombre à une autre (décimale, fractionnaire, sous forme de pourcentage).
- Utiliser un ordre de grandeur pour contrôler un résultat.
- Effectuer une application numérique d'une formule mathématique (longueurs, aires, volumes) ou d'une formule simple provenant d'une autre discipline.
- Résoudre une équation du premier degré du type
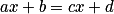 ou
ou 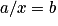 ou une équation du second degré du type
ou une équation du second degré du type 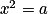 .
.

