Défibrillateur cardiaque, sujet de métropole, mai 2022, exercice au choix C
Énoncé
Exercice sur 5 points
Mots-clés : modèle du circuit RC série
D'après une étude menée par l'université de Lille en 2018, chaque année, environ 46 000 arrêts cardiaques se produisent en dehors des hôpitaux. C'est pourquoi les établissements accueillant du public sont progressivement tenus d'installer un défibrillateur cardiaque.
Cet appareil permet d'appliquer un choc électrique sur le thorax d'un patient dont le cœur se contracte de façon irrégulière et inefficace.
L'objectif de cet exercice est de comprendre le fonctionnement d'un défibrillateur au travers d'un modèle simplifié.
D'après une étude menée par l'université de Lille en 2018, chaque année, environ 46 000 arrêts cardiaques se produisent en dehors des hôpitaux. C'est pourquoi les établissements accueillant du public sont progressivement tenus d'installer un défibrillateur cardiaque.
Cet appareil permet d'appliquer un choc électrique sur le thorax d'un patient dont le cœur se contracte de façon irrégulière et inefficace.
L'objectif de cet exercice est de comprendre le fonctionnement d'un défibrillateur au travers d'un modèle simplifié.
 |
Un défibrillateur installé en lycée
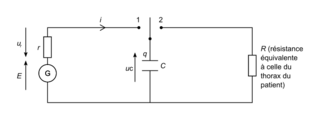
Le circuit électrique d'un défibrillateur cardiaque peut être modélisé de façon simplifiée par le circuit représenté en figure 1 contenant :
Le circuit électrique d'un défibrillateur cardiaque peut être modélisé de façon simplifiée par le circuit représenté en figure 1 contenant :
- un circuit de charge constitué de l'association en série d'un générateur de tension E, d'un conducteur ohmique de résistance r et d'un condensateur de capacité C ;
- un circuit de décharge constitué du condensateur chargé et d'un conducteur ohmique de résistance R équivalente à celle du thorax du patient ;
- un interrupteur à deux positions (1 ou 2) qui permet de fermer soit le circuit de charge soit le circuit de décharge.
 |
On s'intéresse à la charge du condensateur du défibrillateur. À la date t = 0 s, l'utilisateur déclenche la charge du condensateur de capacité C considéré comme initialement totalement déchargé.
1. Indiquer dans quelle position est basculé l'interrupteur pour réaliser la charge du condensateur du circuit schématisé figure 1.
Lors de la charge, le condensateur doit être relié à une source électrique.
2. À l'aide de la loi des mailles, montrer que l'équation différentielle régissant l'évolution de la tension uC(t) aux bornes du condensateur lors de sa charge est :
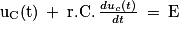
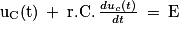
La loi d'Ohm permet de déterminer la tension aux bornes de la résistance. Comme l'intensité du courant est un débit de charges électriques, la loi des mailles permet d'en déduire l'équation différentielle.
3. Vérifier que la solution de cette équation différentielle est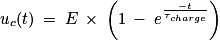 
en précisant l'expression et l'unité de la constante τcharge.
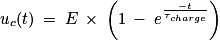en précisant l'expression et l'unité de la constante τcharge.Remplacez la solution donnée dans l'équation différentielle de la question 2.
4. Tracer l'allure de la courbe donnant l'évolution temporelle de la tension aux bornes du condensateur lors de sa charge, en précisant les valeurs de uC(t) à t = 0 s et au bout d'un temps très long.
Les deux valeurs de uc(t) demandées permettent d'établir l'allure de la courbe.
5. Montrer qu'à la date t1 = 5 × τcharge la tension aux bornes du condensateur uC(t) a atteint 99 % de sa valeur finale.
Remplacez la date donnée dans la solution de l'équation différentielle.
On s'intéresse maintenant à la décharge du condensateur et on réalise le montage de la figure 1 avec un conducteur ohmique de résistance R = 10 kΩ et un condensateur de capacité C = 1,5 μF, permettant d'avoir un temps caractéristique proche de celui d'un défibrillateur commercial.
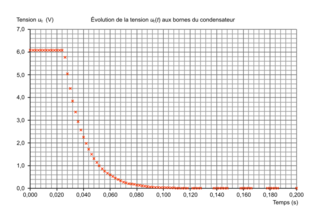
On suit l'évolution de la tension uC(t) aux bornes du condensateur initialement chargé. La courbe expérimentale obtenue est représentée en ANNEXE À RENDRE AVEC LA COPIE.
On suit l'évolution de la tension uC(t) aux bornes du condensateur initialement chargé. La courbe expérimentale obtenue est représentée en ANNEXE À RENDRE AVEC LA COPIE.
6. Déterminer graphiquement l'instant t2 où l'interrupteur a été basculé de la position 1 à la position 2.
La tension aux bornes du condensateur est rapidement modifiée.
7. En faisant apparaître clairement la démarche sur l'ANNEXE À RENDRE AVEC LA COPIE, évaluer graphiquement le temps caractéristique de décharge τgraph. Commenter.
Le temps caractéristique de décharge correspond à la durée nécessaire pour que la tension atteigne 37 % de sa tension initiale.
Sur la notice d'un défibrillateur commercial, les valeurs suivantes sont annoncées :
- durée totale de charge : moins de 10 secondes ;
- durée de délivrance du choc : moins de 4 secondes ;
- tension appliquée à la victime adulte : environ 2 000 V ;
- valeur de la capacité C = 170 μF.
8. Sachant que, dans ces conditions d'utilisation, la résistance électrique offerte par le corps d'un adulte est comprise entre 50 Ω et 150 Ω, estimer la durée nécessaire pour que la décharge du condensateur du défibrillateur soit considérée comme totale. Commenter.
Calculez la durée de la décharge avec les deux résistances.
ANNEXE à rendre avec la copie
 |
Corrigé
1. Pour charger le condensateur, il faut qu'il soit relié au générateur G donc il faut basculer l'interrupteur en position 1.
2. Lors de la charge, on a, d'après la loi des mailles :
uC + ur = E
soit uC + r.i = E
or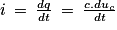
on remplace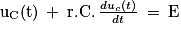
soit uC + r.i = E
or
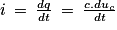
on remplace
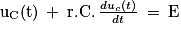
3. La solution donnée est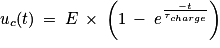 
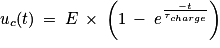
Or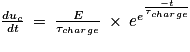 
On remplace :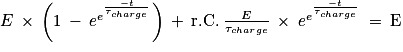
Soit :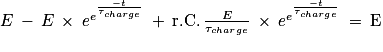
D'où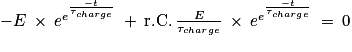
Soit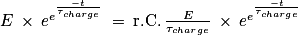
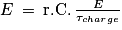
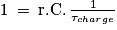
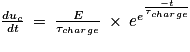
On remplace :
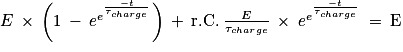
Soit :
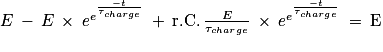
D'où
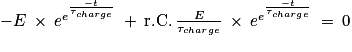
Soit
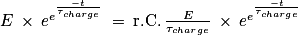
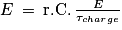
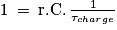
La solution donnée n'est solution de l'équation différentielle que si τcharge = r.C qui représente la constante de temps lors de la charge et qui est en secondes.
4. À t = 0 s,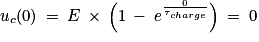
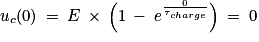
Quand t devient très grand,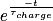 
tend vers 0 donc uc (t) tend vers E.
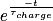tend vers 0 donc uc (t) tend vers E. |
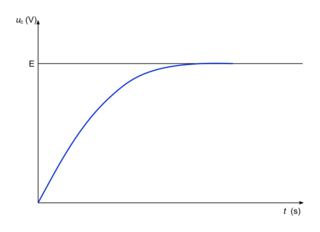5. À la date t1 = 5 × τ
Soit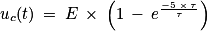 
Soit uc (t) = E × (1 − e−5)
Or (1 − e−5 ) = 0,99
Soit uc (t) = E × 0,99. Il a bien atteint 99 % de sa charge finale au bout de 5 × τ
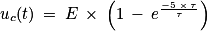
Soit uc (t) = E × (1 − e−5)
Or (1 − e−5 ) = 0,99
Soit uc (t) = E × 0,99. Il a bien atteint 99 % de sa charge finale au bout de 5 × τ
6. L'interrupteur est basculé de la position 1 à la position 2 quand le condensateur commence à se décharger, donc quand uc diminue. On note que le condensateur commence à se décharger à t = 0,024 s.
7. On a uc (0,024) = 6,1 V
Lors de la décharge d'un dipôle RC, le temps caractéristique est égal à la durée nécessaire pour que la tension atteigne 37 % de sa tension initiale.
On cherche le temps caractéristique de décharge correspondant à 6,1 × 0,37 = 2,3 V environ.
On cherche le temps caractéristique de décharge correspondant à 6,1 × 0,37 = 2,3 V environ.
 |
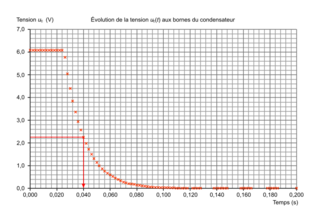τ = 0,040 − 0,024 = 0,016 s
Or R × C = 10 × 103 × 1,5 × 10−6 = 0,015 s
Le temps caractéristique de décharge trouvé graphiquement est en concordance avec le calcul théorique et est très rapide puisque, au bout de 5 × τ = 0,06 s, il est totalement déchargé (à 99 %).
Or R × C = 10 × 103 × 1,5 × 10−6 = 0,015 s
Le temps caractéristique de décharge trouvé graphiquement est en concordance avec le calcul théorique et est très rapide puisque, au bout de 5 × τ = 0,06 s, il est totalement déchargé (à 99 %).
8. Si le corps d'un adulte a une résistance comprise entre 50 Ω et 150 Ω, alors le temps caractéristique de décharge de ce condensateur est compris entre R×C = 50 × 170 × 10−6 = 8,5 × 10−3 s et R×C = 150 × 170 × 10−6 = 2,6 × 10−2 s.
Il sera totalement déchargé au bout de 5 × τ soit entre 0,043 s et 0,128 s.
Si on attend 4 s pour la délivrance du choc, on est sûr que cela sera efficace.
Si on attend 4 s pour la délivrance du choc, on est sûr que cela sera efficace.
