Énoncé
Exercice sur 7 points
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Pour les questions 1 à 3 ci-dessous, on considère une fonction f définie et deux fois dérivable sur .
.
La courbe de sa fonction dérivée f' est donnée ci-dessous.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Pour les questions 1 à 3 ci-dessous, on considère une fonction f définie et deux fois dérivable sur
 .
.La courbe de sa fonction dérivée f' est donnée ci-dessous.
• On admet que f' admet un maximum en 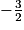 et que sa courbe coupe l'axe des abscisses au point de coordonnées
et que sa courbe coupe l'axe des abscisses au point de coordonnées 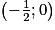 .
.
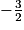 et que sa courbe coupe l'axe des abscisses au point de coordonnées
et que sa courbe coupe l'axe des abscisses au point de coordonnées 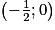 .
.1. On rappelle que la courbe ci-dessous représente la fonction dérivée f' de f.
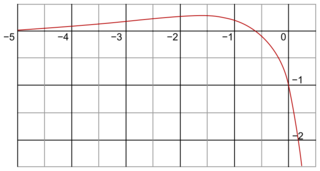 |
a. La fonction f admet un maximum en 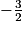
b. La fonction f admet un maximum en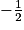
c. La fonction f admet un minimum en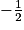
d. Au point d'abscisse −1, la courbe de la fonction f admet une tangente horizontale
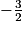
b. La fonction f admet un maximum en
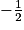
c. La fonction f admet un minimum en
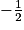
d. Au point d'abscisse −1, la courbe de la fonction f admet une tangente horizontale
Pour répondre à cette question, il faut connaître le lien entre maximum ou minimum d'une fonction courbe et les variations de la fonction dérivée associée. Pour trouver les variations de la dérivée, il faut observer sa représentation, mais ne pas confondre variations et signe de la fonction.
2.
a. La fonction f est convexe sur![\left ]-\infty;-\frac{3}{2}\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m6.png)
b. La fonction f est convexe sur![\left ]-\infty;-\frac{1}{2}\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m7.png)
c. La courbe Cf représentant la fonction f n'admet pas de point d'inflexion
d. La fonction f est concave sur![\left ]-\infty;-\frac{1}{2}\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m8.png)
a. La fonction f est convexe sur
![\left ]-\infty;-\frac{3}{2}\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m6.png)
b. La fonction f est convexe sur
![\left ]-\infty;-\frac{1}{2}\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m7.png)
c. La courbe Cf représentant la fonction f n'admet pas de point d'inflexion
d. La fonction f est concave sur
![\left ]-\infty;-\frac{1}{2}\right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m8.png)
La convexité d'une fonction dépend du signe de sa dérivée seconde et donc aussi des variations de sa dérivée. En observant la représentation graphique de la dérivée de la fonction, on obtient les variations de cette dérivée et on peut donc répondre à la question.
3. La dérivée seconde f'' de la fonction f vérifie :
a. f''(x) 0 pour
0 pour ![x\in \left ]-\infty ;-\frac{1}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m9.png)
b. f''(x) 0 pour
0 pour ![x\in \left [-2 ;-1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m10.png)
c.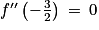
d. f''(−3) = 0
a. f''(x)
 0 pour
0 pour ![x\in \left ]-\infty ;-\frac{1}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m9.png)
b. f''(x)
 0 pour
0 pour ![x\in \left [-2 ;-1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m10.png)
c.
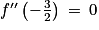
d. f''(−3) = 0
Le signe de la dérivée seconde d'une fonction dépend des variations de sa dérivée. En observant la représentation graphique de la dérivée de la fonction, on obtient les variations de cette dérivée et donc on peut répondre à la question.
4. On considère trois suites (un), (vn) et (wn). On sait que, pour tout entier naturel n, on a : un  vn
vn  wn et de plus :
wn et de plus : 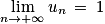 et
et 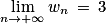 . On peut alors affirmer que :
. On peut alors affirmer que :
a. la suite (vn) converge
b. si la suite (un) est croissante alors la suite (vn) est minorée par u0
c. 1 v0
v0  3
3
d. la suite (vn) diverge
 vn
vn  wn et de plus :
wn et de plus : 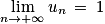 et
et 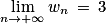 . On peut alors affirmer que :
. On peut alors affirmer que :a. la suite (vn) converge
b. si la suite (un) est croissante alors la suite (vn) est minorée par u0
c. 1
 v0
v0  3
3d. la suite (vn) diverge
Il faut bien connaître les différentes propriétés de convergence et de limites d'une suite pour ne pas tomber dans les pièges des différentes réponses proposées.
5. On considère une suite (un) telle que, pour tout entier naturel n non nul : 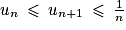 .
.
On peut alors affirmer que :
a. la suite (un) diverge
b. la suite (un) converge
c.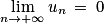
d.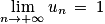
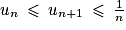 .
.On peut alors affirmer que :
a. la suite (un) diverge
b. la suite (un) converge
c.
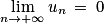
d.
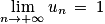
Il faut bien connaître les différentes propriétés de convergence et de limites d'une suite pour ne pas tomber dans les pièges des différentes réponses proposées. Il faut raisonner comme lors d'une récurrence et éliminer les différentes propositions fausses ou impossibles au fur et à mesure.
6. On considère (un) une suite réelle telle que, pour tout entier naturel n, on a : n < un < n + 1. On peut affirmer que :
a. Il existe un entier naturel N tel que uN est un entier
b. la suite (un) est croissante
c. la suite (un) est convergente
d. la suite (un) n'a pas de limite
a. Il existe un entier naturel N tel que uN est un entier
b. la suite (un) est croissante
c. la suite (un) est convergente
d. la suite (un) n'a pas de limite
Il faut bien connaître les différentes propriétés de convergence et de limites d'une suite pour ne pas tomber dans les pièges des différentes réponses proposées. Il faut raisonner comme lors d'une récurrence et éliminer les différentes propositions fausses ou impossibles au fur et à mesure.
Corrigé
1. Réponse b : la fonction f admet un maximum en 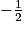
Par lecture graphique, la dérivée est positive sur![\left ]-\infty ; -\frac{1}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m18.png) et négative sur
et négative sur ![\left ]-\frac{1}{2};+\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m19.png) ; f est donc croissante puis décroissante : elle admet donc un maximum en
; f est donc croissante puis décroissante : elle admet donc un maximum en 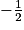 .
.
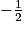
Par lecture graphique, la dérivée est positive sur
![\left ]-\infty ; -\frac{1}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m18.png) et négative sur
et négative sur ![\left ]-\frac{1}{2};+\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m19.png) ; f est donc croissante puis décroissante : elle admet donc un maximum en
; f est donc croissante puis décroissante : elle admet donc un maximum en 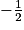 .
.2. Réponse a : la fonction f est convexe sur ![\left ]-\infty ; -\frac{3}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m21.png)
Comme la fonction f' est croissante sur![\left ]-\infty ; -\frac{3}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m22.png) , on en déduit que la fonction f est convexe sur cet intervalle.
, on en déduit que la fonction f est convexe sur cet intervalle.
![\left ]-\infty ; -\frac{3}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m21.png)
Comme la fonction f' est croissante sur
![\left ]-\infty ; -\frac{3}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m22.png) , on en déduit que la fonction f est convexe sur cet intervalle.
, on en déduit que la fonction f est convexe sur cet intervalle.3. Réponse c : 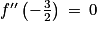
On a déjà vu que la fonction f' est croissante sur![\left ]-\infty ; -\frac{3}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m24.png) . De plus, elle est décroissante sur
. De plus, elle est décroissante sur ![\left ]-\frac{3}{2};+\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m25.png) , on en déduit donc que
, on en déduit donc que 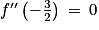 .
.
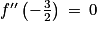
On a déjà vu que la fonction f' est croissante sur
![\left ]-\infty ; -\frac{3}{2} \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m24.png) . De plus, elle est décroissante sur
. De plus, elle est décroissante sur ![\left ]-\frac{3}{2};+\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde25_m25.png) , on en déduit donc que
, on en déduit donc que 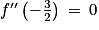 .
.4. Réponse b : si la suite (un) est croissante alors la suite (vn) est minorée par u0
Si la suite (un) est croissante, on a pour tout , u0
, u0  un
un  vn et donc la suite (vn) est elle aussi minorée par u0.
vn et donc la suite (vn) est elle aussi minorée par u0.
Si la suite (un) est croissante, on a pour tout
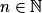 , u0
, u0  un
un  vn et donc la suite (vn) est elle aussi minorée par u0.
vn et donc la suite (vn) est elle aussi minorée par u0.5. Réponse b : la suite (un) converge
Pour tout entier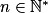 , on a
, on a 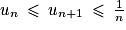 , la suite (un) est donc croissante.
, la suite (un) est donc croissante.
D'autre part : pour n ≠ 0, on peut écrire :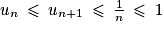 .
.
Conclusion : la suite (un) est croissante et elle majorée par 1, d'après la propriété des suites, elle est donc convergente.
Pour tout entier
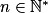 , on a
, on a 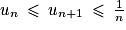 , la suite (un) est donc croissante.
, la suite (un) est donc croissante.D'autre part : pour n ≠ 0, on peut écrire :
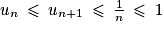 .
.Conclusion : la suite (un) est croissante et elle majorée par 1, d'après la propriété des suites, elle est donc convergente.
6. Réponse b : la suite (un) est croissante
On a, au rang n, l'inégalité : n < un < n + 1 et, au rang n + 1, on a l'inégalité : n + 1<un+1 < n + 2, ainsi, on obtient : un < n + 1 < un+1 et donc la suite (un) est croissante.
On a, au rang n, l'inégalité : n < un < n + 1 et, au rang n + 1, on a l'inégalité : n + 1<un+1 < n + 2, ainsi, on obtient : un < n + 1 < un+1 et donc la suite (un) est croissante.

