Énoncé
Partie 1
Un point lumineux se déplace sur une droite à partir de l'origine. À chaque seconde, il se déplace d'une unité vers la droite avec la probabilité p, ou vers la gauche avec la probabilité 1 −p, les déplacements étant supposés indépendants. On note X son abscisse après n secondes. Quelle est la loi de X et son espérance ?Il pourra être utile d'introduire la suite de variables aléatoires
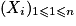 , où Xi est la variable aléatoire qui vaut 1 si le i-ème déplacement s'effectue vers la droite, et −1 si ce déplacement s'effectue vers la gauche, et de considérer Yi la variable aléatoire définie par
, où Xi est la variable aléatoire qui vaut 1 si le i-ème déplacement s'effectue vers la droite, et −1 si ce déplacement s'effectue vers la gauche, et de considérer Yi la variable aléatoire définie par 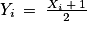 .
.Partie 2
Soit n un entier naturel non nul. Soit 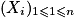 , une suite de variables aléatoires de Bernoulli indépendantes de paramètre
, une suite de variables aléatoires de Bernoulli indépendantes de paramètre ![p\: \in \: ]0\: ;\: 1[](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m4.png) . On note
. On note 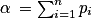 .
.
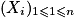 , une suite de variables aléatoires de Bernoulli indépendantes de paramètre
, une suite de variables aléatoires de Bernoulli indépendantes de paramètre ![p\: \in \: ]0\: ;\: 1[](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m4.png) . On note
. On note 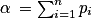 .
.1. Montrer que 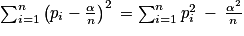 .
.
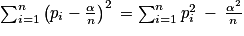 .
.2. Calculer 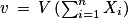 .
.
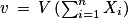 .
.3. Déterminer les valeurs de pi maximisant v.
La bonne méthode
Partie 1
On utilise l'indication de l'énoncé et on se ramène à une situation binomiale pour faciliter les calculs.Partie 2
1. Il suffit de développer l'expression de gauche pour obtenir celle de droite.
2. On n'oublie pas que les variables sont indépendantes et qu'elles suivent toutes une loi de Bernoulli.
3. Il suffit de mettre en relation les deux premières questions.
Corrigé
Partie 1
En suivant l'indication de l'énoncé, on écrit que 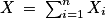 . Par ailleurs, pour tout entier naturel i compris entre 1 et n, Xi = 1 si et seulement si
. Par ailleurs, pour tout entier naturel i compris entre 1 et n, Xi = 1 si et seulement si 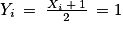 , et Xi = −1 si et seulement si
, et Xi = −1 si et seulement si 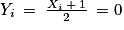 . On en déduit que
. On en déduit que 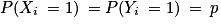 et
et 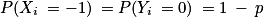 . La variable Yi est donc la variable de Bernoulli de paramètre p. Les variables Yi sont mutuellement indépendantes puisque les Xi le sont.
. La variable Yi est donc la variable de Bernoulli de paramètre p. Les variables Yi sont mutuellement indépendantes puisque les Xi le sont.
Soit la variable Y définie par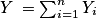 . La variable Y est la somme de n variables indépendantes de Bernoulli de même paramètre p. Ainsi, Y suit la loi binominale de paramètres n et p. On en déduit que
. La variable Y est la somme de n variables indépendantes de Bernoulli de même paramètre p. Ainsi, Y suit la loi binominale de paramètres n et p. On en déduit que ![Y(\Omega)= \left [ 0\: ;\: n \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m14.png) .
.
On a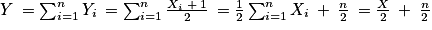 , soit X = 2Y − n. L'ensemble des valeurs prises par X est donc l'ensemble
, soit X = 2Y − n. L'ensemble des valeurs prises par X est donc l'ensemble ![\left \{ 2k\: -\: n,\: k\: \in \left [ 0\: ;\: n \right ] \right \}\: = \left \{ -n\: ;\: 2\: -\: n\: ;\: 4\: -\: n\: ;\cdots \: ;\: n\: -\: 4\: ;\: n\: -\: 2\: ;\: n \right \}](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m16.png) .
.
Quel que soit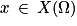 , il existe
, il existe ![k\: \in \: [1\: ;\: n]](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m18.png) tel que x = 2k − n, et :
tel que x = 2k − n, et :
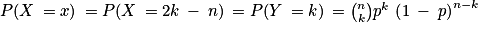 .
.
Ainsi, on obtient la loi de X :
Quel que soit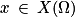 ,
, 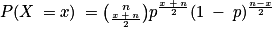 .
.
S'agissant de l'espérance de X, il serait extrêmement maladroit d'utiliser la loi de X pour l'obtenir, on peut contourner la difficulté de deux manières :
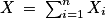 . Par ailleurs, pour tout entier naturel i compris entre 1 et n, Xi = 1 si et seulement si
. Par ailleurs, pour tout entier naturel i compris entre 1 et n, Xi = 1 si et seulement si 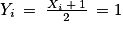 , et Xi = −1 si et seulement si
, et Xi = −1 si et seulement si 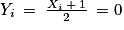 . On en déduit que
. On en déduit que 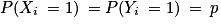 et
et 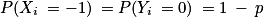 . La variable Yi est donc la variable de Bernoulli de paramètre p. Les variables Yi sont mutuellement indépendantes puisque les Xi le sont.
. La variable Yi est donc la variable de Bernoulli de paramètre p. Les variables Yi sont mutuellement indépendantes puisque les Xi le sont.Soit la variable Y définie par
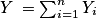 . La variable Y est la somme de n variables indépendantes de Bernoulli de même paramètre p. Ainsi, Y suit la loi binominale de paramètres n et p. On en déduit que
. La variable Y est la somme de n variables indépendantes de Bernoulli de même paramètre p. Ainsi, Y suit la loi binominale de paramètres n et p. On en déduit que ![Y(\Omega)= \left [ 0\: ;\: n \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m14.png) .
.On a
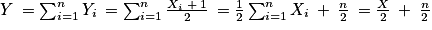 , soit X = 2Y − n. L'ensemble des valeurs prises par X est donc l'ensemble
, soit X = 2Y − n. L'ensemble des valeurs prises par X est donc l'ensemble ![\left \{ 2k\: -\: n,\: k\: \in \left [ 0\: ;\: n \right ] \right \}\: = \left \{ -n\: ;\: 2\: -\: n\: ;\: 4\: -\: n\: ;\cdots \: ;\: n\: -\: 4\: ;\: n\: -\: 2\: ;\: n \right \}](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m16.png) .
.Quel que soit
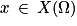 , il existe
, il existe ![k\: \in \: [1\: ;\: n]](https://static1.assistancescolaire.com/t/images/t_spemat_rde17_m18.png) tel que x = 2k − n, et :
tel que x = 2k − n, et :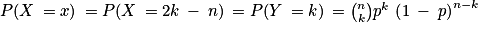 .
.Ainsi, on obtient la loi de X :
Quel que soit
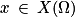 ,
, 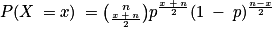 .
.S'agissant de l'espérance de X, il serait extrêmement maladroit d'utiliser la loi de X pour l'obtenir, on peut contourner la difficulté de deux manières :
• E(X) = E(2Y − n) = 2E(Y) − n, par linéarité de l'espérance, et comme E(Y) = np, on trouve E(X) = 2(np) − n = n (2p − 1).
• Une autre façon de procéder est de calculer E(X1) = −1 × (1 − p) + 1 × p = 2p − 1, et d'utiliser que 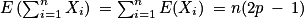 .
.
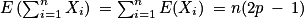 .
.Partie 2
1. On a :
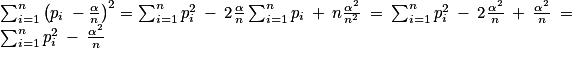 .
.
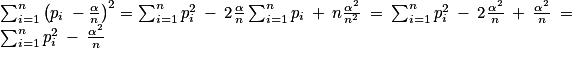 .
.2. Comme chaque variable Xi suit la loi de Bernoulli de paramètre pi, on a E(Xi) = pi et 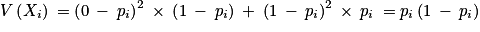 .
.
Par ailleurs, les variables sont indépendantes, donc :
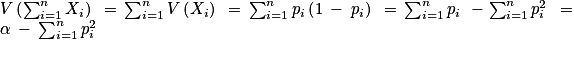
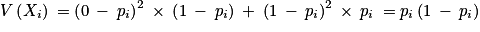 .
.Par ailleurs, les variables sont indépendantes, donc :
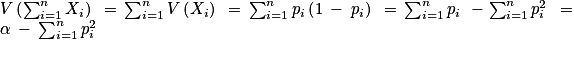
3. La formule précédente montre que la variance est maximale lorsque 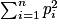 est minimale. Or,
est minimale. Or, 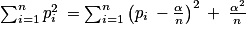 , donc
, donc 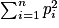 est minimale pour
est minimale pour 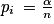 .
.
La variance de X est maximale pour les pi tous égaux à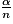 . La loi de X est alors la loi binomiale de paramètres n et
. La loi de X est alors la loi binomiale de paramètres n et 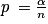 .
.
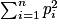 est minimale. Or,
est minimale. Or, 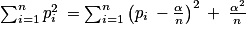 , donc
, donc 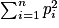 est minimale pour
est minimale pour 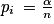 .
.La variance de X est maximale pour les pi tous égaux à
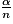 . La loi de X est alors la loi binomiale de paramètres n et
. La loi de X est alors la loi binomiale de paramètres n et 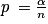 .
.
