• Tout nombre décimal peut s'écrire sous la forme d'une fraction décimale, (une fraction décimale a pour numérateur, un entier et pour dénominateur, 10, 100, 1 000, etc.).
Ainsi, 1,2 peut s'écrire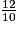 
.
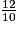.Le nombre de zéros au dénominateur correspond au nombre de décimales.
4,62 =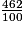 
(2 décimales ← 2 zéros)
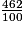(2 décimales ← 2 zéros)• De même, on peut toujours donner l'écriture décimale d'une fraction décimale.
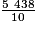= 543,8 (1 zéro ← 1 décimale)
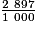= 2,897 (3 zéros ← 3 décimales)5 +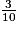 
+ 
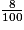= 5 + 0,3 + 0,08 = 5,38
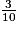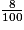+ = 5 + 0,3 + 0,08 = 5,38Exercice n°1
Donne l'écriture décimale la plus simple des nombres suivants.
Écrivez les réponses dans les zones colorées.
a.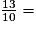 
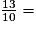
b.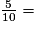 
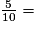
c.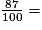 
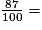
d.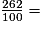 
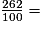
e.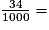 
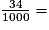
f.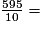 
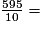
• Le nombre de zéros au dénominateur correspond au nombre de décimales du nombre en écriture décimale.
• Tu peux aussi effectuer les divisions.
Par exemple : 34 ÷ 1 000 = 0,034.
Par exemple : 34 ÷ 1 000 = 0,034.
Exercice n°2
Écris les nombres suivants sous forme décimale.
Écrivez les réponses dans les zones colorées.
a. 31 +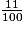 
=
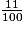= b. 9 +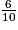 
+ 
=
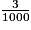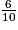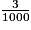+ = c. 7 +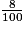 
+ 
=
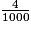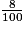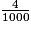+ = Par exemple, 11 centièmes s'écrit 0,11 sous forme décimale.
Exercice n°3
Combien d'unités, de dixièmes, de centièmes et de millièmes, représentent ces écritures ?
Associe à chaque écriture à la bonne combinaison.
Associe à chaque écriture à la bonne combinaison.
Faites glisser les étiquettes dans les zones prévues à cet effet.
2 unités et 3 centièmes
6 unités, 5 dixièmes, 2 centièmes et 6 millièmes
65 unités, 2 dixièmes, et 6 millièmes
imcAnswer2?
6,526
imcAnswer1?
2 +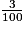 
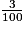
imcAnswer2?
6 +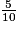 
+ 
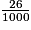
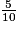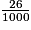
+ imcAnswer1?
2,03
imcAnswer3?
65,206
imcAnswer2?
6 +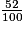 
+ 
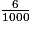
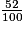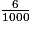
+ imcAnswer3?
65 +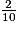 
+ 
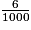
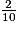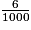
+ Exercice n°4
Coche la bonne réponse.
a. Quel est le nombre décimal égal à 17 +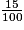 
+ 
?
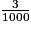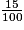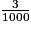+ ? Cochez la bonne réponse.
| ||
| ||
|
b. Quelle est la fraction décimale égale à 0,027 ?
Cochez la bonne réponse.
| ||
| ||
|
+ 
a. 15 centièmes, c'est aussi 1 dixième et 5 centièmes ; le chiffre des dixièmes du nombre cherché est donc 1, son chiffre des centièmes est 5.
b. Pense que 0,027 se lit 0 virgule 027 ou 27 millièmes.
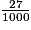
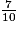
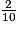