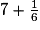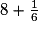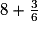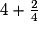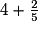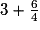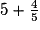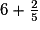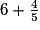Décomposer une fraction comme somme d'un entier et d'une fraction strictement inférieure à 1
Pour décomposer 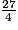 comme la somme d'un entier et d'une fraction strictement inférieure à 1, on commence par chercher le plus grand multiple de 4 (dénominateur de
comme la somme d'un entier et d'une fraction strictement inférieure à 1, on commence par chercher le plus grand multiple de 4 (dénominateur de 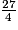 ) inférieur ou égal à 27 (numérateur de
) inférieur ou égal à 27 (numérateur de 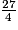 ).
).
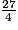 comme la somme d'un entier et d'une fraction strictement inférieure à 1, on commence par chercher le plus grand multiple de 4 (dénominateur de
comme la somme d'un entier et d'une fraction strictement inférieure à 1, on commence par chercher le plus grand multiple de 4 (dénominateur de 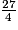 ) inférieur ou égal à 27 (numérateur de
) inférieur ou égal à 27 (numérateur de 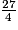 ).
).On calcule les multiples de 4 : 4 × 1 = 4 ; 4 × 2 = 8 ; 4 × 3 = 12 ; 4 × 4 = 16 ; 4 × 5 = 20 ; 6 × 4 = 24 ; 7 × 4 = 28.
La réponse est donc 4 × 6 = 24.
La réponse est donc 4 × 6 = 24.
27 = 24 + 3 donc : 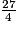 =
= 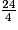 +
+ 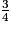 = 6 +
= 6 + 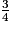 et on a bien
et on a bien 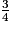 < 1.
< 1.
L'écriture de la fraction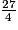 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 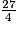 = 6 +
= 6 + 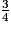 .
.
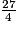 =
= 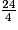 +
+ 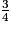 = 6 +
= 6 + 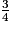 et on a bien
et on a bien 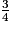 < 1.
< 1.L'écriture de la fraction
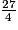 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 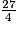 = 6 +
= 6 + 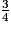 .
.Exercice n°1
Quelle est la décomposition de 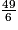 comme somme d'un entier et d'une fraction strictement inférieure à 1 ?
comme somme d'un entier et d'une fraction strictement inférieure à 1 ?
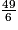 comme somme d'un entier et d'une fraction strictement inférieure à 1 ?
comme somme d'un entier et d'une fraction strictement inférieure à 1 ? Cochez la bonne réponse.
| ||
| ||
|
49 = 48 + 1 = 6 × 8 + 1 donc : 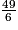 =
= 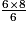 +
+ 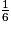 = 8 +
= 8 + 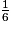 et on a bien
et on a bien 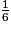 < 1.
< 1.
L'écriture de la fraction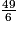 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 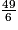 = 8 +
= 8 + 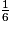 .
.
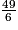 =
= 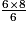 +
+ 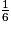 = 8 +
= 8 + 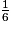 et on a bien
et on a bien 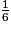 < 1.
< 1.L'écriture de la fraction
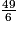 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 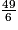 = 8 +
= 8 + 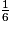 .
.Exercice n°2
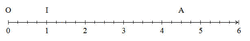 |
Quelle est la décomposition de l'abscisse du point A comme somme d'un entier et d'une fraction strictement inférieure à 1 ?
Cochez la bonne réponse.
| ||
| ||
|
Une unité est composée de quatre graduations. L'abscisse du point A est compris entre 4 et 5, et le point A est situé sur la deuxième graduation après celle du point d'abscisse 4 (sans compter cette graduation).
La décomposition de l'abscisse du point A comme somme d'un entier et d'une fraction strictement inférieure à 1 est donc : 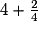 .
.
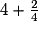 .
.Exercice n°3
La décomposition de 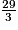 comme somme d'un entier et d'une fraction strictement inférieure à 1 est
comme somme d'un entier et d'une fraction strictement inférieure à 1 est 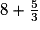 .
.
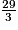 comme somme d'un entier et d'une fraction strictement inférieure à 1 est
comme somme d'un entier et d'une fraction strictement inférieure à 1 est 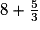 .
. Cochez la bonne réponse.
| ||
|
C'est faux, car 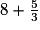 > 1. 29 = 27 + 2 = 3 ×9 + 2 donc
> 1. 29 = 27 + 2 = 3 ×9 + 2 donc 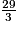 =
= 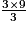 +
+ 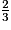 = 9 +
= 9 +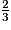 , qui est la bonne décomposition car
, qui est la bonne décomposition car 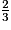 < 1.
< 1.
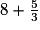 > 1. 29 = 27 + 2 = 3 ×9 + 2 donc
> 1. 29 = 27 + 2 = 3 ×9 + 2 donc 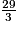 =
= 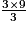 +
+ 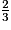 = 9 +
= 9 +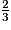 , qui est la bonne décomposition car
, qui est la bonne décomposition car 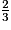 < 1.
< 1.Exercice n°4
Quelle est la décomposition de 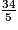 comme somme d'un entier et d'une fraction strictement inférieure à 1 ?
comme somme d'un entier et d'une fraction strictement inférieure à 1 ?
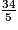 comme somme d'un entier et d'une fraction strictement inférieure à 1 ?
comme somme d'un entier et d'une fraction strictement inférieure à 1 ? Cochez la bonne réponse.
| ||
| ||
|
34 = 30 + 4 = 5 × 6 + 4 donc : 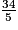 =
= 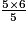 +
+ 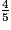 = 6 +
= 6 + 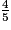 et on a bien
et on a bien 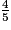 < 1.
< 1.
L'écriture de la fraction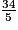 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 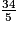 = 6 +
= 6 + 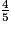 .
.
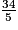 =
= 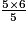 +
+ 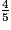 = 6 +
= 6 + 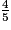 et on a bien
et on a bien 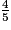 < 1.
< 1.L'écriture de la fraction
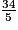 comme somme d'un entier et d'une fraction inférieure à 1 est :
comme somme d'un entier et d'une fraction inférieure à 1 est : 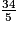 = 6 +
= 6 + 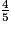 .
.