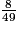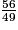Utiliser les termes « quotient, écriture fractionnaire, fraction »
• Le quotient de a par b (non nul) est le nombre, qui multiplié par b, donne a.
L'écriture fractionnaire de ce quotient est :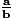
.
L'écriture fractionnaire de ce quotient est :
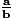.Exemple : l'écriture fractionnaire du quotient de 2,1 par 0,7 est :
 |
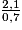= 2,1 ÷ 0,7 = 3 et 3 × 0,7 = 2,1.• Il existe plusieurs écritures fractionnaires d'un même quotient.
3 ÷ 4 = 0,75
0,75 est le quotient de 3 par 4, mais 0,75 est aussi :
= 
= 
= …
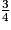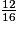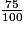Ces écritures sont des fractions car le numérateur et le dénominateur sont des nombres entiers.
3 ÷ 4 = 0,75
0,75 est le quotient de 3 par 4, mais 0,75 est aussi :
- le quotient de 12 par 16,
- le quotient de 75 par 100, etc.
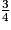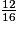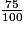= = = …Ces écritures sont des fractions car le numérateur et le dénominateur sont des nombres entiers.
Exercice n°1
Complète avec des mots choisis dans cette liste : « quotient », « dividende », « numérateur », « dénominateur », « décimale », « fractionnaire », « fraction ».
Écrivez les réponses dans les zones colorées.
1. L'écriture 1 ÷ 3 désigne un nombre appelé .
2. Ce nombre peut aussi s'écrire à l'aide d'une barre :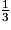 
.
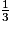est l'écriture de ce nombre.
Dans la mesure où le 1 et le 3 sont des nombres entiers, on peut aussi dire que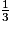
est une .
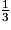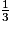. est l'écriture de ce nombre. Dans la mesure où le 1 et le 3 sont des nombres entiers, on peut aussi dire que
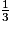est une .Exercice n°2
Réponds aux questions suivantes.
Le quotient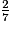 
est une fraction car 2 et 7 sont des entiers.
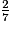est une fraction car 2 et 7 sont des entiers. Cochez la bonne réponse.
| ||
|
Quel est le dénominateur de la fraction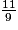 
?
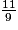? Cochez la bonne réponse.
| ||
| ||
|
Complète l'égalité avec le nombre qui convient : 7 ×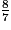 
=
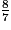= Cochez la bonne réponse.
| ||
| ||
|
Il faut toujours penser à simplifier avant d'effectuer un calcul sur des fractions.
