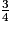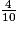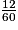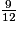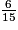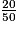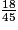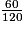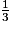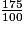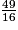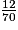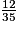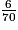Signaler une erreur
Mathématiques - Réviser une notion
Reconnaître des quotients égaux
Mathématiques - Réviser une notion
Reconnaître des quotients égaux
Imprimer
Mathématiques - Réviser une notion
Reconnaître des quotients égaux
Mathématiques - Réviser une notion
Reconnaître des quotients égaux
• 2 × 0,5 = 1 donc 0,5 = 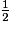 .
.
De même, 4 × 0,5 = 2 donc 0,5 =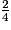 .
.
On en déduit que :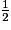 =
= 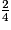 .
.
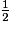 .
.De même, 4 × 0,5 = 2 donc 0,5 =
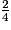 .
.On en déduit que :
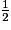 =
= 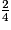 .
.• On remarque que l'on peut passer d'un quotient à l'autre en multipliant numérateur et dénominateur par le même nombre, par exemple, 2 : 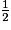 =
= 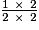 =
= 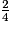 .
.
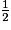 =
= 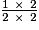 =
= 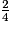 .
.De même, le quotient n'est pas changé lorsqu'on divise numérateur et dénominateur par un même nombre non nul.
• On veut écrire un quotient égal à 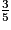 , qui ait pour dénominateur 20.
, qui ait pour dénominateur 20.
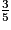 , qui ait pour dénominateur 20.
, qui ait pour dénominateur 20.Cette recherche peut se traduire ainsi : 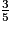 =
= 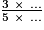 =
= 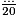 .
.
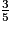 =
= 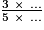 =
= 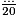 .
.On remarque que : 5 × 4 = 20.
On peut donc compléter l'égalité : 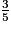 =
= 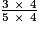 =
= 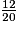 .
.
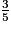 =
= 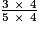 =
= 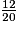 .
.Exercice n°1
Parmi les quotients suivants, quels sont ceux qui sont égaux à 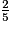 ? (Il y a quatre bonnes réponses.)
? (Il y a quatre bonnes réponses.)
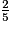 ? (Il y a quatre bonnes réponses.)
? (Il y a quatre bonnes réponses.) Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
| ||
| ||
|
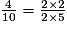
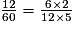
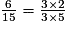
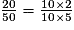
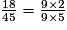
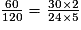
Exercice n°2
Réponds aux questions.
a. Quelle est la fraction égale à 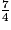 ?
?
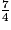 ?
? Cochez la bonne réponse.
| ||
| ||
|
b. Quelle est la fraction égale à 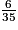 ?
?
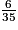 ?
? Cochez la bonne réponse.
| ||
| ||
|
a. 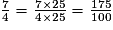
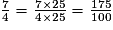
b. 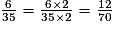
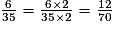
Signaler une erreur
Mathématiques - Réviser une notion
Reconnaître des quotients égaux
Mathématiques - Réviser une notion
Reconnaître des quotients égaux
Imprimer
Mathématiques - Réviser une notion
Reconnaître des quotients égaux
Mathématiques - Réviser une notion
Reconnaître des quotients égaux