Un cercle de centre O et de rayon r est l'ensemble des points situés à r cm du point O.
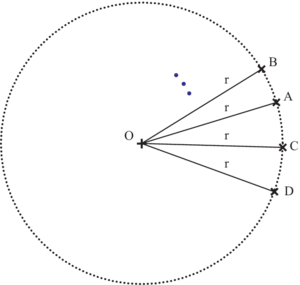 |
Voici un cercle de centre O et de rayon r.
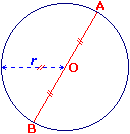 |
• Le segment [AB] qui joint deux points du cercle et qui passe par O est un diamètre. AB = 2 ×r.
• La surface située à l'intérieur du cercle (cercle compris) est un disque.
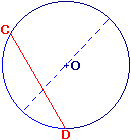
• Si C et D sont deux points du cercle :
- le segment [CD] est une corde ;
- les points C et D délimitent deux arcs de cercles (le bleu clair et le bleu foncé).
 |
Remarque : le diamètre [AB] est une corde particulière.
Exercice n°1
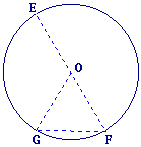
Complète avec les mots qui conviennent.
 |
Écrivez les réponses dans les zones colorées.
1. [EF] est un .
2. [OG] est un .
3. [FG] est une .
1. Les points E et F sont sur le cercle et le segment [EF] passe par le centre du cercle.
2. G est un point du cercle et O est le centre du cercle.
3. F et G sont deux points du cercle.
Exercice n°2
Coche les réponses exactes.
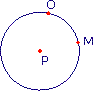 |
1. Le centre du cercle est :
Cochez la bonne réponse.
| ||
| ||
|
2. Le segment [PM] est :
Cochez la bonne réponse.
| ||
| ||
|
Un rayon d'un cercle est un segment joignant le centre du cercle et un point du cercle : [PM] et [PO] sont des rayons.
Exercice n°3
Soit les points A, B, C, D, E, F, I tels que : IA = 6 cm ; IB = 5 cm ; IC = 6 cm ; ID = 2 cm ; IE = 6 cm ; IF = 7 cm.
Complète les phrases suivantes
Complète les phrases suivantes
Écrivez les réponses dans les zones colorées.
a. A est sur un cercle de centre I, les points qui sont sur un même cercle sont : A, , .
b. Le rayon de ce cercle mesure cm.
a. Tu sais que IA = 6 cm. Il faut donc trouver les autres points à 6 cm de I.
b. Le centre est I donc le rayon mesure 6 cm.

