Pour calculer l'aire A d'un rectangle, il faut multiplier la mesure de sa longueur L par la mesure de sa largeur l.
A = L × l
A = L × l
• Exemple :
Une plate-bande de forme rectangulaire fait 2,5 m de long et 60 cm de large. On cherche son aire.
On convertit la largeur en m, puis on calcule l'aire en m2 :
0,6 × 2,5 = 1,5.
0,6 × 2,5 = 1,5.
• Remarque :
Quand on connaît l'aire A d'un rectangle et l'une de ses dimensions (L ou l), on peut retrouver l'autre en utilisant :
L =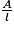
ou l = 
.
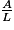L =
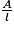ou l = 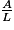.Exercice n°1
Complète le tableau suivant.
Écrivez les réponses dans les zones colorées.
| Longueur (en cm) | 43 | 7,8 | 37 | |
| Largeur (en cm) | 21 | 4,5 | | 6,4 |
| Aire du rectangle (en cm2) | | | 666 | 48 |
• Pour obtenir les aires, on calcule :
43 × 21 (première colonne) ;
7,8 × 4,5 (deuxième colonne).
43 × 21 (première colonne) ;
7,8 × 4,5 (deuxième colonne).
• Pour obtenir la largeur, on calcule :
666 ÷ 37 (troisième colonne).
666 ÷ 37 (troisième colonne).
• Pour obtenir la longueur, on calcule :
48 ÷ 6,4 (quatrième colonne).
48 ÷ 6,4 (quatrième colonne).
Exercice n°2
Quelle est l'affirmation qui convient ?
a. L'aire d'un rectangle de longueur 7 cm et de largeur 5 cm est, en cm2 :
Cochez la bonne réponse.
| ||
| ||
|
b. L'aire d'un triangle rectangle dont les deux côtés perpendiculaires mesurent 2 cm et 3 cm est, en cm2 :
Cochez la bonne réponse.
| ||
| ||
|
a. 5 × 7 = 35
L'aire du rectangle est donc égale à 35 cm2.
L'aire du rectangle est donc égale à 35 cm2.
b.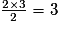 
L'aire du triangle est donc égale à 3 cm2.
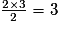
L'aire du triangle est donc égale à 3 cm2.
Exercice n°3
 |
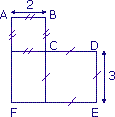Quelle est l'aire du polygone ABCDEF ?
Coche la bonne réponse.
Coche la bonne réponse.
Cochez la bonne réponse.
| ||
| ||
|
Ce polygone est composé de deux carrés et d'un rectangle.
Aire du petit carré : 2 × 2 = 4.
Aire du rectangle : 2 × 3 = 6.
Aire du grand carré : 3 × 3 = 9.
L'aire du polygone est donc égale à 4 + 6 + 9 = 19.
Aire du petit carré : 2 × 2 = 4.
Aire du rectangle : 2 × 3 = 6.
Aire du grand carré : 3 × 3 = 9.
L'aire du polygone est donc égale à 4 + 6 + 9 = 19.
Exercice n°4
L'aire totale d'un appartement est de 60 m2.
Il est composé de deux pièces A et B, dont les dimensions figurent sur le plan ci-dessous.
Il est composé de deux pièces A et B, dont les dimensions figurent sur le plan ci-dessous.
 |
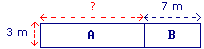Quelle est la longueur de la pièce A ?
Écrivez la réponse dans la zone colorée.
Réponse : m.
• L'aire totale est celle d'un rectangle dont l'une des dimensions est 3 m.
Calcule l'autre dimension.
Calcule l'autre dimension.
• Remarque ensuite que la mesure trouvée correspond à la somme des longueurs des pièces A et B.
• 60 m2 est l'aire d'un rectangle de 3 m de large.
Sa longueur est donc 20 m (60 ÷ 3).
Sa longueur est donc 20 m (60 ÷ 3).
• La longueur de la pièce A est alors 13 m (20 − 7).
