•
 |
Calculons l'aire de la figure A, l'unité d'aire étant ce carré .
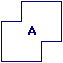 |
Il suffit de recouvrir la figure de carrés unités.
Aire de la figure A : 7 carrés unités.
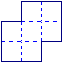 |
• On est parfois conduit à compter en fractions d'unité.
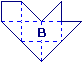
Aire de la figure B : 3 carrés plus 6 moitiés de carré, soit au total : 6 carrés unités.
 |
Exercice n°1
Soient A, B et C les aires des figures a, b et c.
On veut les classer dans l'ordre croissant.
On veut les classer dans l'ordre croissant.
Complète.
Écrivez les réponses dans les zones colorées.
< <
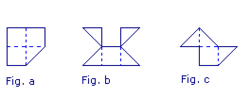 |
• Fig. a : 3 carreaux et 1 demi-carreau (le carreau étant l'unité d'aire).
• Fig. b : 1 carreau et 4 demi-carreaux, donc 3 carreaux entiers.
• Fig. c : 1 carreau et 3 demi-carreaux, donc 2 carreaux et demi.
Exercice n°2
1. Sur une feuille à petits carreaux, trace un triangle EFG, isocèle et rectangle en E, tel que : EF = EG = 5 cm.
2. En utilisant des carrés unités de 5 mm de côté, détermine l'aire de ce triangle.
Écrivez la réponse dans la zone colorée.
Réponse : carrés unités.
• Sur une feuille à petits carreaux, le côté d'un carreau mesure 5 mm.
• Pour déterminer l'aire demandée, il suffit de compter le nombre de carreaux entiers et de demi-carreaux contenus dans le triangle que tu as dessiné.
• Il suffit de compter le nombre de carreaux entiers et le nombre de demi-carreaux.
• Il y a 45 carreaux entiers et 10 demi-carreaux, donc 5 carreaux entiers supplémentaires.
Exercice n°3
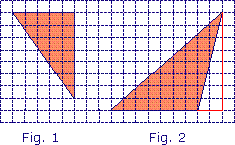
Donne les aires exactes des figures coloriées en utilisant le carreau comme unité.
 |
Écrivez les réponses dans les zones colorées.
• Fig. 1 : carreaux
• Fig. 2 : carreaux
N'oublie pas que deux triangles rectangles forment un rectangle.
Tu obtiens donc l'aire d'un triangle rectangle en divisant celle du rectangle correspondant par 2.
Tu obtiens donc l'aire d'un triangle rectangle en divisant celle du rectangle correspondant par 2.
• L'aire de la figure 1 est 17,5 carreaux : c'est la moitié de 35 carreaux, qui est l'aire du rectangle de longueur 7 et de largeur 5 (mesures des côtés de l'angle droit du triangle).
•
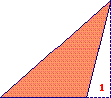 |
Pour calculer l'aire de la figure 2, on reconstitue un triangle rectangle comme sur la figure suivante :
Son aire est 36 carreaux (c'est la moitié d'un rectangle d'aire 8 × 9 soit 72 carreaux). L'aire du petit triangle 1 est 8 carreaux (c'est la moitié de l'aire d'un rectangle d'aire 2 × 8 soit 16 carreaux). L'aire du triangle colorié est donc égale à 36 − , soit 28 carreaux.
Exercice n°4
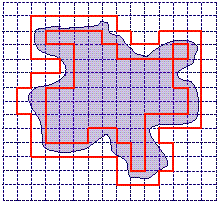
Donne le meilleur encadrement possible de l'aire A de la surface coloriée. Utilise le carreau comme unité.
 |
Écrivez les réponses dans les zones colorées.
< A <
Compte les carreaux à l'intérieur de chacune des deux formes entourées en rouge.
En comptant les carreaux dans chacune des deux formes entourées en rouge, tu trouves 56 < A < 114.
Exercice n°5
 |
Coche la bonne réponse.
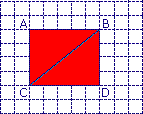
a. Quelle est l'aire, en carreaux, du rectangle ABCD ?
Cochez la bonne réponse.
| ||
| ||
|
b. Quelle est l'aire, en carreaux, du triangle BCD ?
Cochez la bonne réponse.
| ||
| ||
|
a. 5 × 4 = 20
L'aire du rectangle ABCD est donc égale à 20 carreaux.
L'aire du rectangle ABCD est donc égale à 20 carreaux.
b. L'aire du triangle BCD est égale à la moitié de l'aire du rectangle ABCD, soit à 10 carreaux.
Exercice n°6
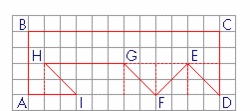 |
u est l'unité d'aire du pavage (correspondant à un petit carré sur le dessin).
Coche la bonne réponse en t'aidant des pointillés.
Coche la bonne réponse en t'aidant des pointillés.
a. Aire de la figure IHGF :
Cochez la bonne réponse.
| ||
| ||
|
b. Aire de la figure FED :
Cochez la bonne réponse.
| ||
| ||
|
c. Aire de la figure ABCD :
Cochez la bonne réponse.
| ||
| ||
|
d. Aire de la figure rouge ABCDEFGHI :
Cochez la bonne réponse.
| ||
| ||
|
a. Il suffit de compter les unités entières et les demi-unités.
L'aire de la figure IHGF est égale 8 unités entières et 4 demi-unités, soit à 10 u.
L'aire de la figure IHGF est égale 8 unités entières et 4 demi-unités, soit à 10 u.
b. L'aire de la figure FED est égale à 2 unités entières et 4 demi-unités, soit à 4 u.
c. 4 × 12 = 48
L'aire de la figure ABCD est égale à 48 u.
L'aire de la figure ABCD est égale à 48 u.
d. 48 − (10 + 4) = 34
L'aire de la figure ABCDEFGHI est égale à 34 u.
L'aire de la figure ABCDEFGHI est égale à 34 u.

