Définition
H est le pied de la perpendiculaire menée de A à d.
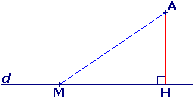 |
La distance de A à d est AH.
- Autrement dit, H est le point de d le plus proche de A.
- Quel que soit le point M de d différent de H, on a : AH < AM.
Application
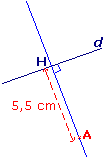
On veut placer un point A à 5,5 cm de la droite d :- On place un point H sur d.
- On construit la perpendiculaire à d qui passe par H.
- Sur cette perpendiculaire, on place A tel que AH = 5,5 cm.
 |
Exercice n°1
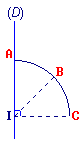 |
Les points A, B et C sont à 4 cm du point I.
Coche le point qui se situe à 4 cm de la droite (D).
Coche le point qui se situe à 4 cm de la droite (D).
Cochez la bonne réponse.
| ||
| ||
|
• La distance d'un point à une droite est la distance entre ce point et son projeté orthogonal sur la droite.
• Seul C est tel que (CI) est perpendiculaire à la droite (D).
Exercice n°2
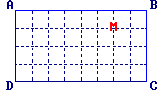 |
ABCD est un rectangle tel que :
AB = 8 et BC = 4.
Indique la distance du point M aux quatre côtés du rectangle.
AB = 8 et BC = 4.
Indique la distance du point M aux quatre côtés du rectangle.
Écrivez les réponses dans les zones colorées.
1. La distance de M à (AB) est .
2. La distance de M à (CD) est .
3. La distance de M à (BC) est .
4. La distance de M à (AD) est .
• L'unité choisie est le côté des petits carrés du quadrillage.
• Il suffit de compter le nombre d'unités qui séparent M de la droite considérée.
Exercice n°3
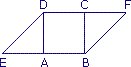 |
Sur la figure ci-contre, ABCD est un carré de 2 cm de côté. E est le symétrique de B par rapport à A et DEBF est un parallélogramme.
Les affirmations suivantes sont-elles vraies ou fausses ?
Coche la bonne réponse.
Coche la bonne réponse.
a. La distance du point B à la droite (DE) est égale à 4 cm.
Cochez la bonne réponse.
| ||
|
b. La distance de F à la droite (AB) est égale à 2 cm.
Cochez la bonne réponse.
| ||
|
c. Si M est un point tel que la distance de M à (AB) est égale à 2 cm alors M appartient à (CD).
Cochez la bonne réponse.
| ||
|
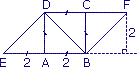 |
c. M peut aussi être situé sur l'autre parallèle à (AB) et située à 2 cm de (AB).
Exercice n°4
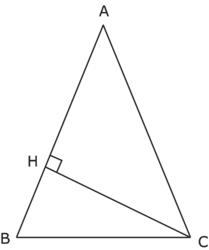
ABC est un triangle isocèle en A tel que AB = 7 cm. L'aire de ce triangle est égale à 8,75 cm2. Quelle est la distance du point C à la droite (AB) ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Trace le triangle ABC et la hauteur relative au côté [AB].
• Trace la hauteur issue de C. La longueur CH représente aussi la distance du point C à la droite (AB).
• Tu connais l'aire du triangle ABC et le côté AB. Calcule la hauteur CH :
Aire (ABC) =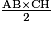
8,75 × 2 = 7 × CH
17,5 ÷ 7 = CH
2,5 = CH.
Aire (ABC) =
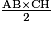
8,75 × 2 = 7 × CH
17,5 ÷ 7 = CH
2,5 = CH.
• La longueur CH représente aussi la distance du point C à la droite (AB).
 |

