La famille Merluche dépense 1 800 € par mois. Les dépenses sont réparties de la façon suivante :
| Charges fixes | Nourriture | Divers |
| 1 044 € | 450 € | 306 € |
| 58% | 25% | 17% |
Pour tracer un diagramme circulaire, on raisonne ainsi :
le budget total est représenté par le disque (360°). Donc 58% du budget total seront représentés par un angle mesurant 58% de 360°, soit 208,8° (arrondi à l'unité : 209°).
On obtient ce diagramme circulaire :
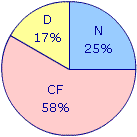 |
CF = Charges fixes
N = Nourriture
D = Divers
N = Nourriture
D = Divers
Les mesures des angles sont proportionnelles aux quantités qu'ils représentent (ici, aux dépenses).
Exercice n°1
Lis les affirmations suivantes.
1. Faire un diagramme circulaire, c'est représenter des données :
Cochez la bonne réponse.
| ||
| ||
|
2. Pour tracer un diagramme circulaire, on utilise le fait que la somme des mesures des angles représentant les valeurs :
Cochez la bonne réponse.
| ||
| ||
|
Voici un exemple de diagramme circulaire :
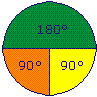 |
180 + 90 + 90 = 360
Exercice n°2
Coche la réponse exacte.
Le diagramme circulaire ci-dessous donne la répartition du temps passé devant la télévision, par jour, par de jeunes collégiens.
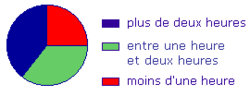 |
Plus de la moitié des élèves regardent plus de deux heures par jour la télévision :
Cochez la bonne réponse.
| ||
| ||
|
Le secteur angulaire bleu, qui représente les élèves regardant la télévision plus de deux heures par jour, fait moins de la moitié du disque.
Exercice n°3
Le diagramme circulaire ci-dessous donne la répartition des réponses à la question « Aimez-vous le chocolat ? » posée à des élèves de collège.
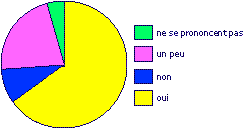 |
Réponds aux questions.
Écrivez les réponses dans les zones colorées.
1. Quelle est la réponse le plus souvent donnée ?
→ C'est la réponse « ».
→ C'est la réponse « ».
2. Y a-t-il beaucoup d'élèves qui ne se prononcent pas ?
→
→
3. Y a-t-il plus de « non » que de « ne se prononcent pas » ?
→
→
La proportion d'élèves qui ne se prononcent pas est la plus faible ; c'est le secteur de disque qui a la petite aire.
Exercice n°4
Le diagramme circulaire ci-dessous donne la répartition des réponses à la question posée à des élèves de collège : « Aimeriez-vous avoir une heure de maths de plus par semaine ? »
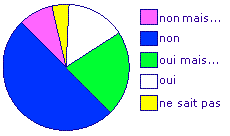 |
Écrivez les réponses dans les zones colorées.
1. Quelle réponse l'emporte ?
→ C'est la réponse « ».
→ C'est la réponse « ».
2. Quelles réponses ont obtenu le plus de suffrages : les « oui » et les « oui mais… » réunis ou bien les « non » et les « non mais… » réunis ?
→ Ce sont les « » et les « … ».
→ Ce sont les « » et les « … ».
La réponse « non » est représentée par un demi-disque, ce qui signifie que 50 % des élèves ont répondu « non ».
Exercice n°5
Dans un collège de 3 600 élèves, 1 890 élèves étudient l'anglais, 1 020 l'allemand et 690 l'espagnol.
On veut construire un diagramme circulaire.
On veut construire un diagramme circulaire.
a. Complète la phrase suivante.
Écrivez la réponse dans la zone colorée.
360° représentent 3 600 élèves, donc 1° représente élèves.
b. Combien vont mesurer les angles représentant les langues étudiées ?
Remplis le tableau suivant.
Remplis le tableau suivant.
Écrivez les réponses dans les zones colorées.
| | Anglais | Allemand | Espagnol |
| Nombre d'élèves | 1890 | 1020 | 690 |
| Angle (en °) | | | |
a. 360° représentent 3 600 élèves donc 1° représente 10 élèves ou 10 élèves sont représentés par 1°.
b. 1 890 = 189 × 10
1 890 élèves sont donc représentés par 189°.
1 890 élèves sont donc représentés par 189°.
Exercice n°6
Voici la répartition des langues étudiées dans un collège de 5 000 élèves.
Complète le tableau permettant de construire un diagramme circulaire.
Complète le tableau permettant de construire un diagramme circulaire.
Écrivez les réponses dans les zones colorées.
| | Anglais | Allemand | Espagnol |
| Nombre d'élèves | 3000 | 1600 | 400 |
| Pourcentage | % | % | % |
| Angle | ° | ° | ° |
• Pour déterminer les pourcentages, commence par écrire quelle fraction du total représente chaque langue puis trouves-en la valeur décimale.
Par exemple, pour l'anglais :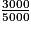 et 3 000 ÷ 5 000 = 0,6 = 60%.
et 3 000 ÷ 5 000 = 0,6 = 60%.
Par exemple, pour l'anglais :
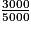 et 3 000 ÷ 5 000 = 0,6 = 60%.
et 3 000 ÷ 5 000 = 0,6 = 60%.• Pour trouver les angles, pense que le disque (360°) représente la totalité des élèves.
Il faut donc appliquer à 360° le pourcentage trouvé.
Il faut donc appliquer à 360° le pourcentage trouvé.
• Sur les 5 000 élèves, 3 000 font de l'anglais.
Le pourcentage correspondant est donc :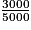 = 0,6 =
= 0,6 = 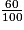 = 60%.
= 60%.
Le pourcentage correspondant est donc :
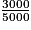 = 0,6 =
= 0,6 = 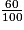 = 60%.
= 60%.• Le disque (360°) représente la totalité des élèves.
Or 60% des élèves font de l'anglais. Ils sont donc représentés par 60% de 360°.
Or 60% des élèves font de l'anglais. Ils sont donc représentés par 60% de 360°.

