Somme ou produit ?

Lorsqu'une expression comporte plusieurs opérations, on peut se demander s'il s'agit d'une somme ou d'un produit.
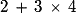
$2\,+\,3\,\times\,4$
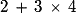
C'est une somme car :

on commence le calcul par la multiplication, elle est prioritaire : 3 × 4 = 12 ;
on effectue l'addition : 2 + 12 = 14.

Règle : pour savoir si une expression est une somme ou un produit, on regarde la dernière opération à effectuer en respectant les règles de priorité :

si c'est une addition ou une soustraction, l'expression est une somme ;
si c'est une multiplication ou une division, l'expression est un produit.

Exemples :

• 2 + 3 + 4 × 4 =
2 + 3 + 16 =
5 + 16.
Il s'agit d'une addition, donc l'expression 2 + 3 + 4 × 4 est une somme.

• 2 × 4 − 25 ÷ 5 =
8 − 5.
Il s'agit d'une soustraction, donc l'expression 2 × 4 − 25 ÷ 5 est une somme.

• (2 + 3 × 4) ÷ (5 − 2) =
(2 + 12) ÷ (3) =
14 ÷ 3.
Il s'agit d'une division, donc l'expression (2 + 3 × 4) ÷ (5 − 2) est un produit.

Exercice n°1

Somme ou produit ? Complète les phrases.

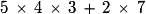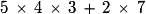L'expression : $5\,\times\,4\,\times\,3\,+\,2\,\times\,7$ est .

L'expression (2 × 3 − 2 ) × 5 + 1 est .

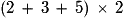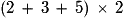L'expression $(2\,+\,3\,+\,5)\,\times\,2$ est .

Exercice n°2

Remplace les espaces vides par le signe mathématique approprié afin d'obtenir ce qui est demandé. (Il y a peut-être plusieurs solutions.)

L'expression : 2 × 4 5 × 6 est une somme.

L'expression : 2 × 5 3 est un produit.

Exercice n°3

Place les parenthèses au bon endroit afin d'obtenir ce qui est demandé. Attention : il ne faut placer qu'un seul couple de parenthèses.

L'expression : 2 + 3 × 5 est un produit.

L'expression : 2 + 3 × 5 est une somme.