Dans un tableau de proportionnalité, les produits en croix sont égaux.
Considérons le tableau suivant :
Considérons le tableau suivant :
 |
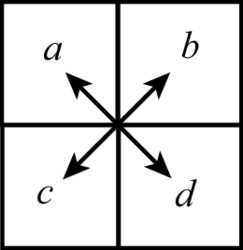Si ce tableau est un tableau de proportionnalité, alors a ×d = b ×c.
La consommation d'eau d'une famille est de 3 150 litres en 9 jours.
On considère que sa consommation moyenne est proportionnelle au nombre de jours.
On considère que sa consommation moyenne est proportionnelle au nombre de jours.
Combien consommera-t-elle en 30 jours ?
• Dressons un tableau de proportionnalité.
| Temps (jours) | 9 | 30 |
| Consommation (L) | 3 150 | ? |
• Dans un tel tableau, les produits en croix sont égaux.
Appelons ? le nombre inconnu.
On a : 9 × ? = 3 150 × 30.
D'où ?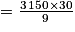
= 10 500.
On a : 9 × ? = 3 150 × 30.
D'où ?
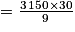= 10 500.• La consommation d'eau de cette famille en 30 jours est de 10 500 L.
Exercice n°1
Calcule la quatrième proportionnelle dans chacun des tableaux.
Écrivez les réponses dans les zones colorées.
| 24 | 40 |
| 7,2 | |
| 10 | 12 |
| | 14,4 |
| 18 | |
| 45 | 75 |
| | 12 |
| 99 | 132 |
Dans un tableau de proportionnalité, les produits en croix sont égaux.
24 × ? = 7 × 40
24 × ? = 288
? = 288 ÷ 24 = 12.
| 24 | 40 |
| 7,2 | ? |
24 × ? = 7 × 40
24 × ? = 288
? = 288 ÷ 24 = 12.
Exercice n°2
Il faut 120 kg d'un minerai de fer pour obtenir 18 kg de fer.
Quelle masse de minerai faut-il pour obtenir 63 kg de fer ?
Écrivez la réponse dans la zone colorée.
• Sur une feuille à part, dresse un tableau de proportionnalité et calcule cette masse en utilisant la règle des « produits en croix ».
• Écris la réponse : kg.
| Minerai | 120 | ? |
| Fer pur | 18 | 63 |
18 × ? = 120 × 63
18 × ? = 7 560
? = 7 560 ÷ 18 = 420.
Exercice n°3
Dans le tableau de proportionnalité suivant, quelle équation doit-on résoudre pour trouver le nombre x ?
| 24 | x |
| 15 | 12 |
Cochez la bonne réponse.
| ||
| ||
|
Pour trouver une quatrième proportionnelle, on écrit les produits en croix égaux, c'est-à-dire : 24 × 12 = 15 × x.
Exercice n°4
On considère l'égalité suivante :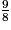 
= 
.
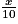Quelle est la valeur du nombre x ?
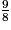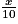= .Quelle est la valeur du nombre x ?
Cochez la bonne réponse.
| ||
| ||
|
Les produits en croix sont égaux, donc 90 = 8 × x ou encore 90 ÷ 8 = x soit x = 11,25.
Exercice n°5
Dans deux litres de jus d'orange, il y a 0,75 L de pulpe. Combien y a-t-il de pulpe dans 25 cL du jus d'orange ?
Cochez la bonne réponse.
| ||
| ||
|
On dresse un tableau de proportionnalité en faisant attention aux unités.
On écrit l'égalité des produits en croix.
200 × x = 75 × 25
x =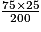
x = 9,375.
| Quantité de jus en cL | 200 | 25 |
| Quantité de pulpe en cL | 75 | x |
On écrit l'égalité des produits en croix.
200 × x = 75 × 25
x =
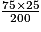
x = 9,375.
Exercice n°6
On considère le tableau suivant :
Quelles sont les valeurs de a et de b ?
| 1,6 | a | 15,7 |
| 9,28 | 15,66 | b |
Quelles sont les valeurs de a et de b ?
Cochez la bonne réponse.
| ||
| ||
|
On utilise les produits en croix.
a × 9,28 = 1,6 × 15,66
a =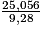
a = 2,7.
a =
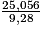
a = 2,7.
b × 2,7 = 15,66 × 15,7
b =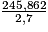
b = 91,06.
b =
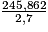
b = 91,06.
