Un avion met 50 min pour faire un trajet de 550 km.
Quelle est sa vitesse moyenne ?
v =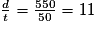 
v = 11 km/min.
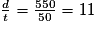
v = 11 km/min.
Si l'avion parcourt 11 km en 1 min, il peut faire 60 × 11 km en 60 min (soit 1 h).
D'où v = 660 km/h.
D'où v = 660 km/h.
Combien de temps l'avion met-il pour faire 825 km, à la même vitesse ?
t =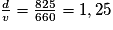 
;
t = 1,25 h ;
t =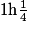
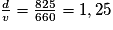;t = 1,25 h ;
t =
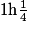
On veut maintenant calculer la distance parcourue par l'avion au cours d'un vol d'1 heure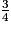 
à la même vitesse de 660 km/h.
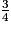à la même vitesse de 660 km/h.• On exprime 1 h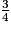 
sous la forme d'un nombre décimal d'heures.
1 h 3/4 = 1,75 h.
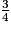sous la forme d'un nombre décimal d'heures.1 h 3/4 = 1,75 h.
• Puis on se sert de la relation entre distance, vitesse et temps.
d = v × t = 660 × 1,75 = 1 155 ; d = 1 155 km.
d = v × t = 660 × 1,75 = 1 155 ; d = 1 155 km.
Exercice n°1
Calcule la distance parcourue par le premier automobiliste et la vitesse moyenne du second.
Écrivez les réponses dans les zones colorées.
1. Un automobiliste a roulé à la vitesse moyenne de 96 km/h pendant une heure et demie.
1 heure et demie correspond au nombre décimal :
La distance qu'il a parcourue est en km :
d = 96 × = .
1 heure et demie correspond au nombre décimal :
La distance qu'il a parcourue est en km :
d = 96 × = .
2. Un autre automobiliste a parcouru 160 km en 1 h 20 min.
Sa vitesse moyenne est en km/min :
v = ÷ = ; soit km/h.
Sa vitesse moyenne est en km/min :
v = ÷ = ; soit km/h.
1. En 1 h, il parcourt 96 km.
En 1,5 h, il parcourt donc (96 × 1,5) km, soit 144 km.
En 1,5 h, il parcourt donc (96 × 1,5) km, soit 144 km.
2. 1 heure 20 min = 80 min.
En 1 min, il parcourt donc (160 ÷ 80) km, soit 2 km.
En 1 h (60 min), il parcourt 60 × 2 km, soit 120 km.
En 1 min, il parcourt donc (160 ÷ 80) km, soit 2 km.
En 1 h (60 min), il parcourt 60 × 2 km, soit 120 km.
Exercice n°2
Quelle égalité est vraie ?
Cochez la bonne réponse.
| ||
| ||
|
On calcule une vitesse moyenne (par exemple 100 km/h) en divisant la distance parcourue (100 km) par le temps mis pour parcourir cette distance (1 h).
De cette formule, on peut déduire celle-ci : temps =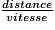
De cette formule, on peut déduire celle-ci : temps =
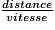
Exercice n°3
Un pilote automobile s'entraîne sur un circuit circulaire de 4 km.
Calcule sa vitesse moyenne puis le temps mis pour effectuer 200 tours.
Calcule sa vitesse moyenne puis le temps mis pour effectuer 200 tours.
Écrivez les réponses dans les zones colorées.
a. Il effectue 70 tours en 1 heure 1/4.
→ Nombre de km parcourus : .
→ Vitesse moyenne : km/h.
→ Nombre de km parcourus : .
→ Vitesse moyenne : km/h.
b. Il veut effectuer 200 tours à la même vitesse.
→ Temps mis : h (la valeur tronquée au dixième) soit heures et demie.
→ Temps mis : h (la valeur tronquée au dixième) soit heures et demie.
a. En 1 h 1/4 (1,25 h), il a parcouru une distance de 280 km.
En 1 h, la distance parcourue est donc de (280 ÷ 1,25) km soit 224 km.
En 1 h, la distance parcourue est donc de (280 ÷ 1,25) km soit 224 km.
b. Pour faire 70 tours, le pilote prend 1,25 h.
Donc pour faire 200 tours, le pilote prend 3,571 4… soit 3,5 h ou 3 h et demie.
Donc pour faire 200 tours, le pilote prend 3,571 4… soit 3,5 h ou 3 h et demie.
Exercice n°4
Coche la réponse exacte.
Une voiture parcourt 35 km à 78 km/h. Pendant combien de temps roule-t-elle ?
Cochez la bonne réponse.
| ||
| ||
|
h
h Cochez la bonne réponse.
| ||
| ||
|
kmOn applique la formule vitesse =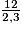 
de laquelle on déduit : distance = vitesse × temps.
Attention, le nombre décimal d'heures correspondant à 2 heures 3 min est 2,5 h.
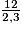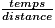
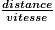
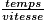
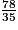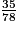de laquelle on déduit : distance = vitesse × temps.Attention, le nombre décimal d'heures correspondant à 2 heures 3 min est 2,5 h.
