Exemple 1
Soit un triangle MNP.
On a MN = 4,8 ; MP = 1,4 ; NP = 5.
On a MN = 4,8 ; MP = 1,4 ; NP = 5.
Le triangle MNP est-il rectangle ?
• Si le triangle est rectangle, alors NP, son plus grand côté, sera l'hypoténuse et on aura :
NP2 = MN2 + MP2.
NP2 = MN2 + MP2.
• On fait le calcul :
NP2 = 25 et MN2 + MP2 = 23,04 + 1,96.
NP2 = 25 et MN2 + MP2 = 23,04 + 1,96.
Les deux résultats sont égaux, donc MNP est rectangle en M.
Exemple 2
Soit un triangle ABC.
On a AB = 5 ; AC = 3,3 ; BC = 6.
On a AB = 5 ; AC = 3,3 ; BC = 6.
Le triangle ABC est-il rectangle ?
• Si le triangle est rectangle, alors BC, son plus grand côté, sera l'hypoténuse et on aura :
BC2 = AB2 + AC2.
BC2 = AB2 + AC2.
• On fait le calcul :
BC2 = 36 et AB2 + AC2 = 25 + 10,89.
BC2 = 36 et AB2 + AC2 = 25 + 10,89.
Les résultats sont différents, donc ABC n'est pas rectangle.
Exercice n°1
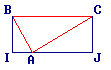 |
IBCJ est un rectangle. A est sur [IJ].
IB = JC = 3 ;
BC = 6,5 ; IA = 2.
Calcule AB2, AC2 et BC2 de façon à prouver que le triangle ABC est rectangle.
IB = JC = 3 ;
BC = 6,5 ; IA = 2.
Calcule AB2, AC2 et BC2 de façon à prouver que le triangle ABC est rectangle.
Écrivez les réponses dans les zones colorées.
ABI est rectangle en I et ACJ en J, donc :
AB2 = ;
AC2 = ;
AB2 + AC2 = ;
BC2 = ;
ABC est rectangle en .
AB2 = ;
AC2 = ;
AB2 + AC2 = ;
BC2 = ;
ABC est rectangle en .
• AB2 = BI2 + IA2 = 9 + 4 = 13.
AC2 = CJ2 + JA2 = 9 + 20,25.
AC2 = CJ2 + JA2 = 9 + 20,25.
• 13 + 29,25 = 42,25.
BC2 = 6,52 = 42,25.
BC2 = 6,52 = 42,25.
Exercice n°2
Indique, dans chacun des deux cas suivants, si ABC est rectangle.
1. AB = 5 ; AC = 3 ; BC = 4.
Écrivez les réponses dans les zones colorées.
AB2 = ; AC2 + BC2 = + = .
Réponse :
Cochez la bonne réponse.
| ||
|
2. AB = 2 ; AC = 2,3 ; BC = 3.
Écrivez les réponses dans les zones colorées.
BC2 = ; AB2 + AC2 = + = .
Réponse :
Cochez la bonne réponse.
| ||
|
2. On calcule : BC2 = 9.
AB2 + AC2 = 4 + 5,29 = 9,29.
ABC n'est donc pas un triangle rectangle.
AB2 + AC2 = 4 + 5,29 = 9,29.
ABC n'est donc pas un triangle rectangle.
Exercice n°3
ABC est un triangle tel que AB = 4 cm, AC = 7 cm et BC = 5,75 cm. Ce triangle est-il rectangle ?
Cochez la bonne réponse.
| ||
| ||
|
• Applique la réciproque du théorème de Pythagore au triangle ABC. Le côté le plus long est AC.
• AC2 = 72 = 49
AB2 + BC2 = 42 + 5,752 = 49,0625.
Ces deux résultats ne sont pas égaux, le triangle ABC n'est pas un triangle rectangle.
AB2 + BC2 = 42 + 5,752 = 49,0625.
Ces deux résultats ne sont pas égaux, le triangle ABC n'est pas un triangle rectangle.

