• Une pyramide est un solide dont la base est un polygone et les faces latérales sont des triangles ayant un sommet commun.
• Une pyramide est régulière lorsque sa base est un polygone régulier et que sa hauteur passe par le centre du polygone de base.
Les faces latérales d'une pyramide régulière sont des triangles isocèles superposables.
• Le volume V d'une pyramide est donné par la formule :
V =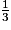 × aire de la base × hauteur.
× aire de la base × hauteur.
V =
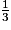 × aire de la base × hauteur.
× aire de la base × hauteur.• Lien entre la pyramide et le patron
Pyramide SABCD
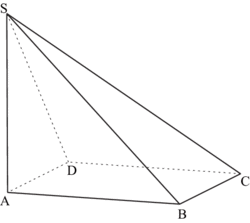 |
Un patron de la pyramide SABCD
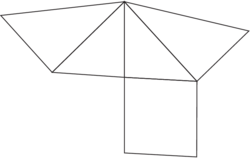 |
Exercice n°1
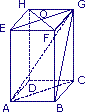 |
Le solide ci-dessus est un pavé droit.
Coche les réponses exactes.
Coche les réponses exactes.
1. Trouve deux pyramides à base triangulaire et de hauteur [GC] :
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
|
2. Trouve une pyramide régulière à base carrée :
Cochez la bonne réponse.
| ||
| ||
|
2. La pyramide ABCDO est régulière : sa base est un polygone régulier et sa hauteur passe par le centre du polygone de base.
Exercice n°2
Calcule le volume ou le côté demandé.
Écrivez les réponses dans les zones colorées.
1. Une pyramide régulière a une base carrée de côté 10 m ; sa hauteur mesure 9 m.
Son volume est égal à m3.
Son volume est égal à m3.
2. Une autre pyramide régulière de base carrée a une hauteur de 11 m et un volume de 132 m3.
Le côté de sa base mesure m.
Le côté de sa base mesure m.
1. V = 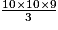 = 300
= 300
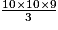 = 300
= 300 2. 132 = 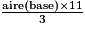
aire (base) =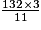 = 36
= 36
La base est un carré de 36 m2, donc de côté 6 m.
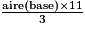
aire (base) =
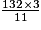 = 36
= 36La base est un carré de 36 m2, donc de côté 6 m.
Exercice n°3
Soit une pyramide régulière de base carrée.
Son arête latérale mesure 8 m, le côté de sa base 4 m.
Son arête latérale mesure 8 m, le côté de sa base 4 m.
Calcule sa hauteur h puis son volume V.
Écrivez les réponses dans les zones colorées.
a. On se place dans le triangle rectangle formé par l'arête, la hauteur et la demi-diagonale du carré de base.
h = m (arrondi au centième)
h = m (arrondi au centième)
b. On en déduit son volume V.
V = m3 (arrondi au centième)
V = m3 (arrondi au centième)
a. La diagonale du carré de base 4 mesure, en m, 4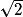 .
.
On applique la propriété de Pythagore : 82 = h2 + (2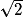 )2 et h2 = 56.
)2 et h2 = 56.
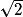 .
.On applique la propriété de Pythagore : 82 = h2 + (2
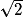 )2 et h2 = 56.
)2 et h2 = 56. b. V = 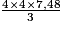 = 39,89
= 39,89
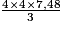 = 39,89
= 39,89Exercice n°4
Soit SABCD une pyramide à base rectangulaire.
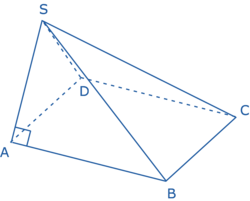 |
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
|
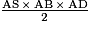 .
.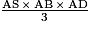 .
.
