1re application
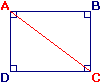
On veut calculer la mesure de la diagonale AC du rectangle ABCD .
AB = 4 et BC = 3.
AB = 4 et BC = 3.
On applique la propriété de Pythagore dans le triangle ABC rectangle en B.
 |
AC2 = AB2 + BC2
Donc : AC2 = 16 + 9 = 25.
On obtient : AC = BD = 5.
Donc : AC2 = 16 + 9 = 25.
On obtient : AC = BD = 5.
2e application
On veut calculer la mesure de [AH], hauteur du triangle isocèle en A.
AB = AC = 10 et BC = 16.
AB = AC = 10 et BC = 16.
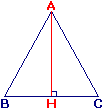 |
• [AH] est hauteur et médiatrice, donc BH = 16 ÷ 2 = 8.
• ABH est rectangle en H, donc :
AH2 = 100 − 64 = 36 ;
AH = 6.
AH2 = 100 − 64 = 36 ;
AH = 6.
Exercice n°1
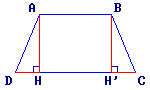 |
ABCD est un trapèze isocèle de bases [AB] et [CD] et de hauteur [AH].
AB = 15 ; DC = 25 ; AD = BC = 13.
Calcule les longueurs ci-dessous.
AB = 15 ; DC = 25 ; AD = BC = 13.
Calcule les longueurs ci-dessous.
Écrivez les réponses dans les zones colorées.
1. DH = CH' = .
2. AH = BH' = .
• HH' = AB = 15, donc DH = CH' = (25 − 15) ÷ 2 = 5.
• AHD est rectangle en H donc AD2 = AH2 + HD2 ;
169 = AH2 + 25 ;
alors AH2 = 144 et AH = 12.
169 = AH2 + 25 ;
alors AH2 = 144 et AH = 12.
Exercice n°2
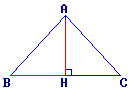 |
ABC est isocèle en A et de hauteur AH.
On sait que :
AB = AC = 4,5 ;
BC = 7,2.
Calcule les longueurs ci-dessous.
On sait que :
AB = AC = 4,5 ;
BC = 7,2.
Calcule les longueurs ci-dessous.
Écrivez les réponses dans les zones colorées.
1. BH = .
2. AH2 = .
3. AH = .
• ABC est isocèle en A, donc H est le milieu de [BC].
• ABH est rectangle en H, donc AB2 = BH2 + HA2 ;
soit 20,25 = 12,96 + HA2 ;
AH2 = 7,29 ; AH =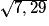 .
.
soit 20,25 = 12,96 + HA2 ;
AH2 = 7,29 ; AH =
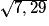 .
.Exercice n°3
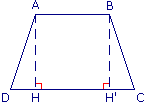 |
ABCD est un trapèze isocèle de bases [AB] et [CD] et de hauteur [AH].
AB = 15 ; DC = 25 ; AD = BC = 13.
AB = 15 ; DC = 25 ; AD = BC = 13.
Calcule les longueurs ci-dessous.
Écrivez les réponses dans les zones colorées.
a. DH = CH' = .
b. AH = BH' = .
a. On a DC = 25 et AB = HH' = 15 donc DH + H'C = 10.
On en déduit que DH = 5.
On en déduit que DH = 5.
b. On applique alors la propriété de Pythagore au triangle AHD rectangle en H :
AD2 = DH2 + AH2
169 = 25 + AH2
AH2 = 169 − 25
AH2 = 144
AH = 12.
AD2 = DH2 + AH2
169 = 25 + AH2
AH2 = 169 − 25
AH2 = 144
AH = 12.
Exercice n°4
Coche la bonne réponse.
La médiane d'un triangle équilatéral de côté 2 cm a pour valeur 1,7 cm (arrondie au dixième).
Cochez la bonne réponse.
| ||
|
ABC est un triangle rectangle tel que AC = 4,3 cm. I est le milieu de [BC]. On sait que AI est égal à 2,5 cm. Le côté [AB] mesure alors 2,55 cm (arrondi au centième).
Cochez la bonne réponse.
| ||
|
Un carré a pour côté 3 cm. Sa diagonale mesure 5 cm.
Cochez la bonne réponse.
| ||
|
Applique le théorème de Pythagore au triangle donné.
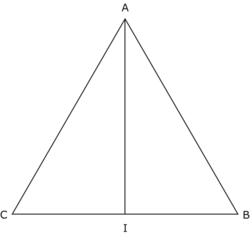 |
• Dans un triangle équilatéral, la médiane est confondue avec la hauteur. Applique le théorème de Pythagore au triangle ACI rectangle en I.
AC2 = CI2 + AI2 or CI est la moitié de BC.
22 = 12 + AI2
4 − 1 = AI2
3 = AI2
AI est égal à 1,732…
AC2 = CI2 + AI2 or CI est la moitié de BC.
22 = 12 + AI2
4 − 1 = AI2
3 = AI2
AI est égal à 1,732…
• AI est la moitié de BC, donc BC = 2 × 2,5 = 5 cm.
Applique le théorème de Pythagore au triangle ABC.
BC2 = AB2 + AC2
25 = AB2 + 4,32
AB2 = 25 − 18,49
AB2 = 6,51
AB = 2,5514…
Applique le théorème de Pythagore au triangle ABC.
BC2 = AB2 + AC2
25 = AB2 + 4,32
AB2 = 25 − 18,49
AB2 = 6,51
AB = 2,5514…
• La diagonale d du carré vérifie d2 = 32 + 32 = 9 + 9 = 18.
d = 4,2426…
d = 4,2426…

