Énoncé 1
Le rayon d'un atome d'azote est de 0,079 nm (nanomètres).
Combien faut-il mettre d'atomes bout à bout pour avoir une file de 4 mm ?
• 0,079 nm = 0,079 × 10−6 mm
Le diamètre d'un atome d'azote est donc égal à 2 × 0,079 × 10−6 mm.
Le diamètre d'un atome d'azote est donc égal à 2 × 0,079 × 10−6 mm.
• Nombre d'atomes dans une file de 4 mm :
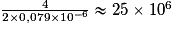(25 millions).
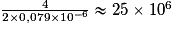(25 millions). Énoncé 2
La vitesse de la lumière est d'environ 3 × 105 km/s.
Quelle est la distance parcourue par la lumière en un an ?
• Dans une année, il y a :
365 × 24 × 3 600 secondes.
365 × 24 × 3 600 secondes.
• Le nombre de km parcourus par la lumière en 1 an est donc égal à :
365 × 24 × 3 600 × 3 × 105, soit 946 080 × 107 km.
365 × 24 × 3 600 × 3 × 105, soit 946 080 × 107 km.
Exercice n°1
Résous le problème ci-dessous.
Combien de temps faudrait-il à un vaisseau spatial pour atteindre l'étoile la plus proche de la Terre (Proxima du Centaure à 40 mille milliards de km) s'il se déplaçait à une vitesse de 50 000 km/h ?
Écrivez la réponse dans la zone colorée.
Sachant qu'il y a 8 760 heures dans une année, la réponse est : ans (arrondi à l'unité).
Utilise la formule : vitesse =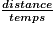 
donc temps =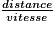 
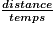donc temps =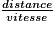 Soit t le temps cherché, t est égal en heures à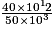 
soit à 0,8 × 109 ou 800 000 000.
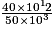soit à 0,8 × 109 ou 800 000 000.Or, il y a environ 8 760 heures dans un an. On trouve 91 324 années.
Exercice n°2
Le rayon terrestre R est d'environ 6 400 km. La distance de la Terre au Soleil est d'environ 23 400 × R. La lumière parcourt environ 300 000 km par seconde. Quel est le temps mis par la lumière pour parcourir la distance du Soleil à la Terre ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
La distance du Soleil à la Terre est égale à 23 400 × 6 400 = 14 976 × 104 km.
Le temps mis est égal à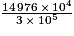
=
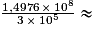0,5 × 103 s.
Le temps mis est égal à
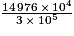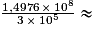= 0,5 × 103 s.
