• On sait qu'un nombre peut s'écrire de différentes façons avec une puissance de 10.
596 000 = 596 × 103
596 000 = 59,6 × 104
596 000 = 5,96 × 105
596 000 = 59,6 × 104
596 000 = 5,96 × 105
• Parmi ces écritures, celle qu'on appelle scientifique est celle qui ne comporte qu'un seul chiffre non nul avant la virgule.
596 000 = 5,96 × 105
0,000 478 = 4,78 × 10−4
459,123 × 102 = 4,591 23 × 104
0,000 478 = 4,78 × 10−4
459,123 × 102 = 4,591 23 × 104
• Pour obtenir la notation scientifique d'un nombre, on peut utiliser les touches EE ou EXP des calculatrices.
Attention à bien interpréter le résultat !
Par exemple :
5.96 − 03 signifie 5,96 × 10−3.
5.96 − 03 signifie 5,96 × 10−3.
Exercice n°1
Quelle est l'écriture scientifique des nombres suivants ?
Coche la bonne réponse.
Coche la bonne réponse.
a. 3 428 =
Cochez la bonne réponse.
| ||
|
b. 32,45 =
Cochez la bonne réponse.
| ||
|
c. 0,0753 =
Cochez la bonne réponse.
| ||
|
d. 17 280 000 =
Cochez la bonne réponse.
| ||
|
e. 345,1 × 102 =
Cochez la bonne réponse.
| ||
|
À chaque fois, la virgule a été déplacée de n rangs, vers la gauche ou vers la droite ; commence par les compter, la puissance de 10 est égale à ce nombre n.
Si la virgule a été déplacée vers la gauche, la puissance est positive. Si la virgule a été déplacée vers la droite, la puissance est négative.
Si la virgule a été déplacée vers la gauche, la puissance est positive. Si la virgule a été déplacée vers la droite, la puissance est négative.
Exercice n°2
Coche la bonne réponse.
L'écriture scientifique de 12 × 107 × 15 × 104 est égale à 1,8 × 1013.
Cochez la bonne réponse.
| ||
|
L'écriture scientifique de 12 × 107 + 15 × 104 est égale à 27 × 1011.
Cochez la bonne réponse.
| ||
|
L'écriture scientifique de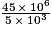 
est égale à 9 × 103.
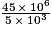est égale à 9 × 103. Cochez la bonne réponse.
| ||
|
• 12 × 107 × 15 × 104 = (12 × 15) × 107 × 104 = 180 × 107 + 4 = 180 × 1011 =1,8 × 1013.
• 12 × 107 + 15 × 104 = 12 × 104 × 103 + 15 × 104 = 104(12 000 + 15) = 12 015 × 104 = 1,2015 × 108.
• 
= 
× 
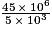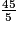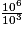= 9 × 106 − 3 = 9 × 103 = 9 000 = 9 × 103.
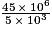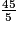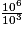= × = 9 × 106 − 3 = 9 × 103 = 9 000 = 9 × 103.
