Donner une valeur approchée d'un quotient de deux nombres relatifs
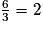
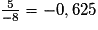
2 et −0,625 sont des valeurs exactes.
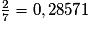…• De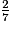 
, on ne peut donner qu'une valeur approchée.
Ainsi, à 0,1 près :
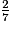, on ne peut donner qu'une valeur approchée. Ainsi, à 0,1 près :
- sa valeur approchée par défaut est 0,2 donc 0,20 ;
- sa valeur approchée par excès est 0,3 donc 0,30.
• Pour en donner la troncature au dixième, on « coupe » l'écriture après le chiffre des dixièmes.
On obtient : 0,2.
On obtient : 0,2.
• Pour en donner l'arrondi au dixième, on tient compte du chiffre des centièmes.
0,28 est plus proche de 0,30 que de 0,20. L'arrondi au dixième de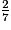
est donc 0,3.
0,28 est plus proche de 0,30 que de 0,20. L'arrondi au dixième de
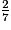est donc 0,3.Exercice n°1
Coche la troncature ou l'arrondi à la précision demandée.
On considère le quotient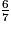 
.
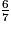. 1. Sa troncature au centième est :
Cochez la bonne réponse.
| ||
| ||
|
2. Son arrondi au centième est :
Cochez la bonne réponse.
| ||
| ||
|
3. Son arrondi à l'unité est :
Cochez la bonne réponse.
| ||
| ||
|
1. Pour obtenir la troncature au centième, on « coupe » après le chiffre des centièmes.
2. 0,857 est plus proche de 0,860 que de 0,850.
3. 0,8 est plus proche de 1 que de 0.
Exercice n°2
Indique la valeur approchée ou l'arrondi à la précision demandée.
Écrivez les réponses dans les zones colorées.
1. Une valeur approchée à 0,01 près :
- de
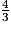par défaut est ; - de
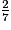par excès est .
2. Un arrondi à 0,1 près :
- de
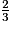est ; - de
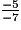est .
1. 
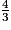= 1,333 333 33…
1,33 < 1,333… < 1,34
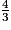= 1,333 333 33…1,33 < 1,333… < 1,34
2. 
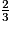= 0,666 666 66…
0,66 est plus proche de 0,70 que de 0,60.
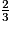= 0,666 666 66…0,66 est plus proche de 0,70 que de 0,60.
Exercice n°3
Donne, à l'aide de ta calculatrice, la valeur décimale approchée par défaut au centième des nombres suivants :
Écrivez les réponses dans les zones colorées.
A =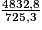 
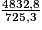
B =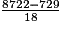 
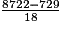
C =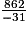 
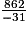
• Explication Le quotient d'un nombre positif par un nombre négatif, donne un nombre négatif.
• La valeur décimale approchée par défaut au millième de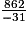 
est −27,806 ; tu peux en déduire que sa valeur approchée par défaut au centième est −27,81.
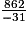est −27,806 ; tu peux en déduire que sa valeur approchée par défaut au centième est −27,81.Exercice n°4
Complète le tableau suivant.
Écrivez les réponses dans les zones colorées.
| Quotient |  |  |  |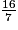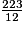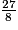
| Troncature au centième | | | |
| Arrondi au centième | | | |
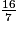
2,285 ; 5 est le chiffre des millièmes, par convention l'arrondi au centième de 2,285 est 2,29.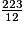 
18,583 ; 3 étant le chiffre des millièmes, l'arrondi au centième de 18,583 est égal à sa troncature c'est-à-dire à 18,58. 
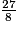
3,375 ; on raisonne comme pour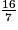 
.Exercice n°5
Coche la bonne réponse.
a. Si 3 est la troncature d'un nombre x au dixième, alors :
Cochez la bonne réponse.
| ||
| ||
|
b. Si 3 est l'arrondi d'un nombre x au dixième, alors :
Cochez la bonne réponse.
| ||
| ||
|
a. Si 3 est la troncature au dixième de x, alors 3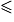 
x < 3 + 0,1.
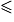x < 3 + 0,1. b. Si 3 est l'arrondi au dixième de x, alors 3 − 0,05 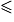x < 3 + 0,05.
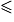x < 3 + 0,05.
