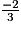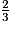Cas d'équations ne comportant qu'un terme en x
| 3x + 5,2 | = −7,7 |
| 3x | = −7,7 − 5,2 |
| 3x | = −12,9 |
| x | = 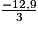 donc x = −4,3 donc x = −4,3 |
Il faut parfois faire des calculs préalables.
| −5 + 4x − 3 | = −11 + 7 |
| 4x − 5 − 3 | = −4 |
| 4x − 8 | = −4 |
| 4x | = −4 + 8 |
| 4x | = 4 |
| x | = 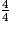 donc x = 1 donc x = 1 |
Cas d'équations comportant plusieurs termes en x
2x − 6 = 5x + 3
On regroupe, d'un côté du signe égal, les termes en x ; de l'autre, les termes sans x.
| 2x − 5x | = 3 + 6 |
| −3x | = 9 |
Puis on isole l'inconnue x.
x =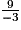 soit x = −3.
soit x = −3.
x =
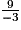 soit x = −3.
soit x = −3.Exercice n°1
Résous les équations suivantes, puis coche le bon résultat.
a. 3x + 3 − 17 = 4
Cochez la bonne réponse.
| ||
| ||
|
b. 19 + 5x − 18 = 76
Cochez la bonne réponse.
| ||
| ||
|
c. 57 + 6x − 2 = 175
Cochez la bonne réponse.
| ||
| ||
|
a. 3x + 3 − 17 = 4
3x − 14 = 4
3x = 4 + 14
3x = 18
x = 18 ÷ 3
x = 6
3x − 14 = 4
3x = 4 + 14
3x = 18
x = 18 ÷ 3
x = 6
b. 19 + 5x − 18 = 76
5x + 1 = 76
5x = 76 − 1
5x = 75
x = 75 ÷ 5
x = 15
5x + 1 = 76
5x = 76 − 1
5x = 75
x = 75 ÷ 5
x = 15
c. 57 + 6x − 2 = 175
6x + 55 = 175
6x = 120
x = 120 ÷ 6
x = 20
6x + 55 = 175
6x = 120
x = 120 ÷ 6
x = 20
Exercice n°2
Complète la résolution des deux équations suivantes.
Écrivez les réponses dans les zones colorées.
a. 3 − 6 + x = 2x − 7
+ x = 2x − 7
2x − x =
Donc x = .
+ x = 2x − 7
2x − x =
Donc x = .
b. − 2 × (x + 9) = 12 + x
Donc x = .
Donc x = .
b. En développant le membre de gauche, on obtient :
− 2x − 18 = 12 + x
− 3x = 18 + 12
x =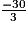 .
.
− 2x − 18 = 12 + x
− 3x = 18 + 12
x =
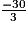 .
.Exercice n°3
Coche les réponses exactes.
1. L'équation 3x − 2 = 0 admet pour solution :
Cochez la bonne réponse.
| ||
| ||
|
2. L'équation 5x − 1 = x + 7 admet pour solution :
Cochez la bonne réponse.
| ||
| ||
|
1. 3x − 2 = 0
3x = 2
x =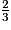
3x = 2
x =
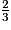
2. 5x − 1 = x + 7
5x − x = 7 + 1
4x = 8
x =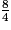
x = 2
5x − x = 7 + 1
4x = 8
x =
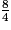
x = 2
Exercice n°4
Le nombre −3 est-il solution de l'équation proposée ?
a. 5x + 1 = 8 − 2x
Cochez la bonne réponse.
| ||
|
b. 7x + 18 = x
Cochez la bonne réponse.
| ||
|
c. 0x = 0
Cochez la bonne réponse.
| ||
|
d. −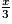 = 0
= 0
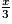 = 0
= 0 Cochez la bonne réponse.
| ||
|
c. −3, comme n'importe quel autre nombre, est solution de 0x = 0.
d. −3 ÷ (−3) = 1.
Exercice n°5
Résous les équations suivantes.
Utilise le signe / pour la barre de fraction.
Utilise le signe / pour la barre de fraction.
Écrivez les réponses dans les zones colorées.
a. 4x − 5 = 2x + 3
Solution : x =
Solution : x =
b. 3 − (6 − x) = 2x + 7
Solution : x =
Solution : x =
c. 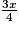 + 1 = 2x −
+ 1 = 2x − 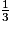
Solution : x =
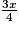 + 1 = 2x −
+ 1 = 2x − 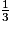
Solution : x =
d. 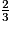 (x + 9) = x
(x + 9) = x
Solution : x =
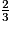 (x + 9) = x
(x + 9) = xSolution : x =
Pour résoudre une équation de type ax = b (a 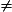 0), on multiplie chaque membre de l'équation par
0), on multiplie chaque membre de l'équation par 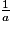 .
.
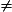 0), on multiplie chaque membre de l'équation par
0), on multiplie chaque membre de l'équation par 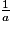 .
.