Énoncé
18 points
Cet exercice est un questionnaire à choix multiple (QCM). Pour chaque question, trois réponses (A, B ou C) sont proposées. Une seule réponse est exacte. Recopier sur la copie le numéro de la question et la lettre correspondant à la réponse exacte. Aucune justification n’est demandée.
Cet exercice est un questionnaire à choix multiple (QCM). Pour chaque question, trois réponses (A, B ou C) sont proposées. Une seule réponse est exacte. Recopier sur la copie le numéro de la question et la lettre correspondant à la réponse exacte. Aucune justification n’est demandée.
| Question | Réponse A | Réponse B | Réponse C |
|---|---|---|---|
| 1. On considère la fonction f définie par f(x) = 3x − 2. Quelle est l’image de −4 par cette fonction ? | −14 | −10 | −3 |
Vous devez remplacer la lettre x dans l’expression par le nombre −4 proposé pour cette question et effectuer le calcul en pensant aux règles de calcul avec les nombres relatifs.
| Question | Réponse A | Réponse B | Réponse C |
|---|---|---|---|
| 2. Combien vaut (−5)3 ? | −125 | −15 | 125 |
Pour ce type de question, il faut gagner du temps en utilisant sa calculatrice pour obtenir directement la réponse recherchée (en pensant à bien écrire les parenthèses).
| Question | Réponse A | Réponse B | Réponse C | |
|---|---|---|---|---|
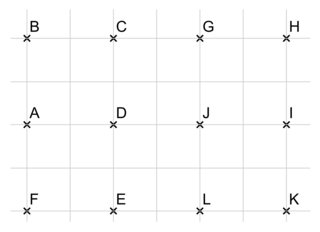
3. Quelle est l’image du point J par la translation qui transforme C en A ?
| H | E | D |
Dans cette question, il faut connaître les caractéristiques géométriques d’une translation (sens et direction) pour les observer sur la figure et les appliquer au point J.
| Question | Réponse A | Réponse B | Réponse C | |
|---|---|---|---|---|
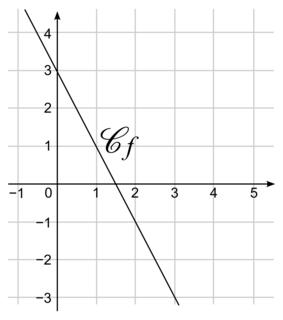
4. Quel est l’antécédent de 3 par la fonction f?
| 3 | −3 | 0 |
Pour déterminer l’antécédent d’un nombre sur la représentation graphique d’une fonction, il faut repérer ce nombre sur l’axe des ordonnées, et observer à quel moment la fonction passe à la hauteur de cette ordonnée pour trouver l’abscisse correspondant à ce point.
| Question | Réponse A | Réponse B | Réponse C |
|---|---|---|---|
| 5. On a mesuré les tailles, en m, de sept élèves : 1,46 ; 1,65 ; 1,6 ; 1,72 ; 1,7 ; 1,67 ; 1,75 Quelle est la médiane, en m, de ces tailles ? | 1,72 | 1,67 | 1,65 |
Il faut connaître la définition de la notion de médiane et bien penser à ranger les valeurs dans l’ordre croissant pour seulement ensuite trouver la valeur centrale de la série.
| Question | Réponse A | Réponse B | Réponse C | |
|---|---|---|---|---|
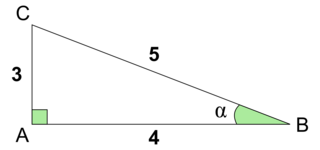
6. Dans le triangle ABC rectangle en A ci-contre, qui n’est pas en vraie grandeur, quelle est la valeur de cosa ?
| 0,8 | 0,75 | 0,6 |
Il faut connaître la formule donnant le cosinus d’un angle aigu dans un triangle rectangle, et surtout ne pas chercher à trouver la valeur de l’angle aigu car c’est souvent ce qui est demandé dans les exercices, mais bien se contenter de trouver la valeur de ce cosinus.
Corrigé
1. On calcule : f(−4) = 3 × (−4) − 2 = −12 − 2 = −14. Réponse A.
2. On calcule : (−5)3 = (−5) × (−5) × (−5) = −125. Réponse A.
3. Si on effectue la translation qui transforme le point C en A, cela signifie que les points glissent une fois vers le bas et vers la gauche. Par la même translation, le point J devient le point E. Réponse B.
4. On voit sur la figure que quand l’ordonnée vaut 3, l’abscisse vaut 0, donc ’antécédent du nombre 3 par la fonction f est 0. Réponse C.
5. On classe les tailles des sept élèves dans l’ordre croissant : 1,46 ; 1,6 ; 1,65 ; 1,67 ; 1,7 ; 1,72 et 1,75.
On voit qu’il y a 7 tailles donc deux groupes de trois élèves, et donc l’élève au milieu de cette série est celui qui mesure 1,67 m. Réponse B.
On voit qu’il y a 7 tailles donc deux groupes de trois élèves, et donc l’élève au milieu de cette série est celui qui mesure 1,67 m. Réponse B.
6. Comme la formule du cosinus est : 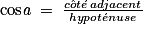 , on calcule donc :
, on calcule donc : 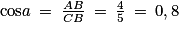 . Réponse A.
. Réponse A.
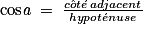 , on calcule donc :
, on calcule donc : 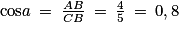 . Réponse A.
. Réponse A.