Énoncé
22 points
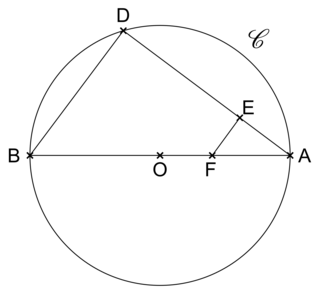
Sur la figure ci-dessous, on a :
• C est un cercle de centre O et de rayon 4,5 cm ;
• [AB] est un diamètre du cercle et D est un point du cercle ;
• les points B, E, A sont alignés, ainsi que les points D, F, A ;
• les droites (BD) et (EF) sont parallèles ;
• BD = 5,4 cm ; DA = 7,2 cm et AE = 2,7 cm.
 |
1. Justifier que le diamètre [AB] mesure 9 cm.
C'est la première question de l'exercice. Il faut connaitre la définition du diamètre d'un cercle et la réponse donnée dans la question permet d'être sûr de son calcul pour continuer l'exercice sereinement. Attention à bien justifier votre réponse !
2. Démontrer que le triangle ABD est rectangle en D.
Ici, il faut se laisser guider par la figure de l'exercice qui nous oriente vers la réciproque d'un théorème fondamental de la géométrie afin de prouver que le triangle est rectangle comme annoncé dans la question.
3. Calculer AF.
Ici, il faut faire appel à l'autre théorème fondamental du programme de cycle 4 et utiliser le parallélisme indiqué dans la consigne pour trouver la mesure recherchée.
4.
a. Justifier que l'aire du triangle ABD est égale à 19,44 cm2.
Pour cette question, il faut connaitre la formule donnant l'aire d'un triangle rectangle (donnée que l'on a obtenue à la question 2) et la réponse donnée dans la question permet d'être sûr de son calcul. Là encore, attention à la justification.
b. Calculer l'aire du disque, arrondie au centième.
Rappel : l'aire du disque est égale à π × R2, où R est le rayon du disque.
Rappel : l'aire du disque est égale à π × R2, où R est le rayon du disque.
Il faut appliquer la formule donnée dans l'exercice pour obtenir l'aire du disque, en faisant attention à la rédaction et à l'arrondi demandé.
5. Quel pourcentage de l'aire du disque représente l'aire du triangle ABD ?
Pour finir cet exercice, on se retrouve à traiter une situation de proportionnalité pour comparer les deux aires obtenues précédemment. Il ne faut pas hésiter à s'appuyer sur un tableau de proportionnalité si la manipulation des fractions s'avère compliquée.
Corrigé
1. On calcule : d = R × 2 = 4,5 × 2 = 9 cm car le diamètre d'un cercle est le double du rayon. Donc le diamètre de ce cercle mesure 9 cm.
2. On a dans un premier temps : AB2 = 92 = 81.
Dans un second temps, on a : AD2 + BD2 = 7,22 + 5,42 = 51,84 + 29,16 = 81.
Alors, on obtient : AB2 = AD2 + BD2.
D'après la réciproque du théorème de Pythagore, on peut en conclure que le triangle ABD est rectangle en D.
Dans un second temps, on a : AD2 + BD2 = 7,22 + 5,42 = 51,84 + 29,16 = 81.
Alors, on obtient : AB2 = AD2 + BD2.
D'après la réciproque du théorème de Pythagore, on peut en conclure que le triangle ABD est rectangle en D.
3. On sait que les droites (EF) et (BD) sont parallèles (d'après l'énoncé). De plus, les points A, F, D et A, E, B sont alignés dans le même ordre.
D'après le théorème de Thalès :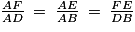
.
Donc, on obtient :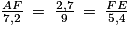
; et ainsi : AF = 7,2 × 2,7 ÷ 9 = 2,16.
Donc le segment [AF] mesure 2,16 cm.
D'après le théorème de Thalès :
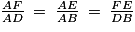.Donc, on obtient :
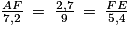; et ainsi : AF = 7,2 × 2,7 ÷ 9 = 2,16.Donc le segment [AF] mesure 2,16 cm.
4.
a. On sait que l'aire d'un triangle rectangle se calcule avec la formule : Aire = L × l ÷ 2, soit Aire = AD × BD ÷ 2 = 7,2 × 5,4 ÷ 2 = 19,44 cm2.
b. On sait que l'aire d'un disque se calcule avec la formule : Aire = π × R2, soit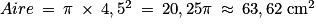 
.
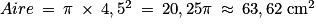.5. On calcule la proportion de l'aire du triangle rectangle par rapport à l'aire du disque :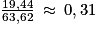 
. L'aire du triangle ABD représente donc 31 % de l'aire du disque.
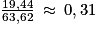. L'aire du triangle ABD représente donc 31 % de l'aire du disque.
