Énoncé
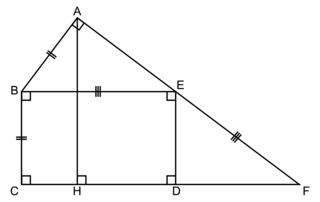
Sur la figure ci-dessous :
• BCDE est un rectangle, BAE est un triangle rectangle en A ;
• la perpendiculaire à la droite (CD) passant par A coupe cette droite en H ;
• les droites (AE) et (CD) se coupent en F.
 |
On donne :
• AB = BC = 4,2 cm ;
• EB = EF = 7 cm.
1. Montrer que l'aire du rectangle BCDE est égale à 29,4 cm2.
C'est la première question de l'exercice. Il faut connaître la formule donnant l'aire d'un rectangle et la réponse donnée dans la question permet d'être sûr de son calcul pour continuer l'exercice sereinement.
2. a. Montrer que la longueur AE est égale à 5,6 cm.
Il faut ici se laisser guider par la figure de l'exercice qui nous oriente vers un théorème fondamental de la géométrie afin de trouver la mesure annoncée dans cette question.
b. Calculer l'aire du triangle rectangle ABE.
Pour répondre à cette question, il faut connaître la formule donnant l'aire d'un triangle rectangle et se souvenir qu'on peut retrouver cette formule grâce à celle du rectangle. En effet, le triangle rectangle s'obtient grâce à un découpage simple d'un rectangle.
3. a. Montrer que les droites (ED) et (HAç) sont parallèles.
Dans cette question de l'exercice, nous n'avons pas assez de mesures pour utiliser le théorème de Thalès, il faut donc chercher dans les notions plus basiques afin de montrer le parallélisme des deux droites.
b. Calculer la longueur AH.
Avec le parallélisme obtenu à la question précédente, il faut se laisser guider par l'exercice et utiliser l'un des théorèmes fondamentaux pour trouver cette mesure.
Corrigé
1. L'aire d'un rectangle est donnée par la formule : A = L × l.
Cela donne : A = 7 × 4,2 = 29,4.
L'aire du rectangle BCDE est donc bien égale à 29,4 cm2.
Cela donne : A = 7 × 4,2 = 29,4.
L'aire du rectangle BCDE est donc bien égale à 29,4 cm2.
2. a. Dans le triangle BAE rectangle en A, on peut appliquer le théorème de Pythagore et on obtient : BE2 = AB2 + AE2.
Ainsi, on a : AE2 = BE2 − AB2 = 72 −4,22 = 49 − 17,64 = 31,36.
Donc, on obtient :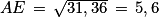 .
.
La longueur AE mesure donc bien 5,6 cm.
Ainsi, on a : AE2 = BE2 − AB2 = 72 −4,22 = 49 − 17,64 = 31,36.
Donc, on obtient :
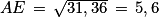 .
.La longueur AE mesure donc bien 5,6 cm.
b. L'aire d'un triangle rectangle est donnée par la formule : 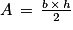 .
.
Cela donne :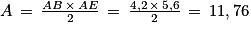 .
.
L'aire du triangle rectangle ABE est donc égale à 11,76 cm2.
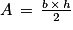 .
.Cela donne :
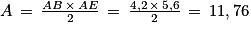 .
.L'aire du triangle rectangle ABE est donc égale à 11,76 cm2.
3. a. Comme les droites (DE) et (AH) sont perpendiculaires à la même troisième droite (CD), on peut conclure que les deux droites (DE) et (AH) sont parallèles entre elles.
b. Dans le triangle AFH, on a :
• les points F, E, A et F, D, H qui sont alignés dans le même ordre ;
• les droites (DE) et (AH) qui sont parallèles.
D'après le théorème de Thalès, on obtient : 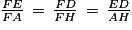 .
.
D'après les données numériques de l'exercice, on sait que FA = FE + EA = 7 + 5,6 = 12,6 cm et que ED = BC = 4,2 cm (car BCDE est un rectangle).
On obtient alors :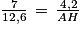 , soit
, soit 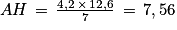 .
.
La longueur AH mesure donc 7,56 cm.
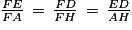 .
.D'après les données numériques de l'exercice, on sait que FA = FE + EA = 7 + 5,6 = 12,6 cm et que ED = BC = 4,2 cm (car BCDE est un rectangle).
On obtient alors :
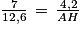 , soit
, soit 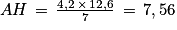 .
.La longueur AH mesure donc 7,56 cm.

