Énoncé
20 points
Une famille se promène au bord d'une rivière.
Les enfants aimeraient connaître la largeur de la rivière.
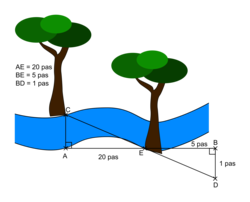
Ils prennent des repères, comptent leurs pas et dessinent le schéma ci-dessous sur lequel les points C, E et D, de même que A, E et B sont alignés. (Le schéma n'est pas à l'échelle.)
Une famille se promène au bord d'une rivière.
Les enfants aimeraient connaître la largeur de la rivière.
Ils prennent des repères, comptent leurs pas et dessinent le schéma ci-dessous sur lequel les points C, E et D, de même que A, E et B sont alignés. (Le schéma n'est pas à l'échelle.)
 |
1. Démontrer que les droites (AC) et (BD) sont parallèles.
C'est la première question de l'exercice et nous n'avons pas assez de mesures pour utiliser le théorème de Thalès, il faut donc chercher dans les notions plus basiques afin de montrer le parallélisme des deux droites.
2. Déterminer, en nombre de pas, la largeur AC de la rivière.
Avec le parallélisme obtenu à la question précédente, il faut se laisser guider par l'exercice et utiliser l'un des théorèmes fondamentaux pour trouver cette mesure.
Pour les questions qui suivent, on assimile la longueur d'un pas à 65 cm.
3. Montrer que la longueur CE vaut 13,3 m, en arrondissant au décimètre près.
À nouveau, on se laisse guider par la figure de l'exercice qui nous guide vers un autre théorème fondamental pour trouver la mesure demandée dans cette question.
4. L'un des enfants lâche un bâton dans la rivière au niveau du point E. Avec le courant, le bâton se déplace en ligne droite en 5 secondes jusqu'au point C.
a) Calculer la vitesse du bâton en m/s.
Vous pouvez procéder de plusieurs manières pour résoudre cette question. On est en présence d'un problème de proportionnalité, il faut donc utiliser les méthodes de calcul appropriées et bien rédiger les étapes de vos calculs.
b) Est-il vrai que « le bâton se déplace à une vitesse moyenne inférieure à 10 km/h » ?
Cette question traite à nouveau un sujet de proportionnalité qui peut donc être résolu de plusieurs façons différentes, mais pour lequel il faut détailler vos calculs.
Il faut également être vigilant lors des conversions nécessaires à la résolution de cette question, car elles sont souvent sources d'erreurs de calcul.
Il faut également être vigilant lors des conversions nécessaires à la résolution de cette question, car elles sont souvent sources d'erreurs de calcul.
Corrigé
1. Les droites (AC) et (BD) sont toutes les deux perpendiculaires à la droite (AB). Ainsi, on en déduit que les droites (AC) et (BD) sont parallèles entre elles.
2. Dans les triangles EAC et EBD, on a :
 Le point E qui appartient aux segments [AB] et [CD] ;
Le point E qui appartient aux segments [AB] et [CD] ;
 Les droites (AC) et (BD) qui sont parallèles.
Les droites (AC) et (BD) qui sont parallèles.
D'après le théorème de Thalès, on obtient :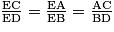 .
.
On obtient alors :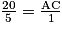 soit AC = 4.
soit AC = 4.
La largeur de la rivière est donc de 4 pas.
 Le point E qui appartient aux segments [AB] et [CD] ;
Le point E qui appartient aux segments [AB] et [CD] ; Les droites (AC) et (BD) qui sont parallèles.
Les droites (AC) et (BD) qui sont parallèles.D'après le théorème de Thalès, on obtient :
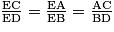 .
.On obtient alors :
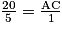 soit AC = 4.
soit AC = 4.La largeur de la rivière est donc de 4 pas.
3. Dans le triangle ACE rectangle en A, on peut appliquer le théorème de Pythagore et on obtient : CE2 = AC2 + AE2. Ainsi, on a : CE2 = 42 + 202 = 16 + 400 = 416.
Donc, on obtient :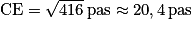 .
.
Comme un pas mesure 65 cm, on obtient :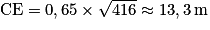 lorsqu'on arrondit au dm près.
lorsqu'on arrondit au dm près.
Donc, on obtient :
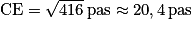 .
.Comme un pas mesure 65 cm, on obtient :
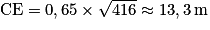 lorsqu'on arrondit au dm près.
lorsqu'on arrondit au dm près.4.
a) La vitesse du bâton est donnée par la formule : 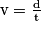 . Ainsi, on a :
. Ainsi, on a : 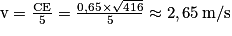 .
.
Remarque : si on prend CE 13,3 m, la vitesse moyenne obtenue est d'environ 2,66 m/s.
13,3 m, la vitesse moyenne obtenue est d'environ 2,66 m/s.
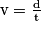 . Ainsi, on a :
. Ainsi, on a : 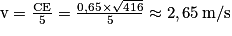 .
.Remarque : si on prend CE
 13,3 m, la vitesse moyenne obtenue est d'environ 2,66 m/s.
13,3 m, la vitesse moyenne obtenue est d'environ 2,66 m/s.b) On sait que 1 km représente 1 000 m et que 1 h compte 3 600 secondes. Ainsi, si on convertit, on obtient : 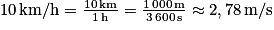 .
.
Ainsi, l'affirmation proposée est exacte, car le bâton se déplace à une vitesse inférieure à 10 km/h.
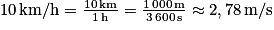 .
.Ainsi, l'affirmation proposée est exacte, car le bâton se déplace à une vitesse inférieure à 10 km/h.

