Énoncé
20 points
Le Futuroscope est un parc de loisirs situé dans la Vienne. L'année 2019 a enregistré 1,9 million de visiteurs.
1. Combien aurait-il fallu de visiteurs en plus en 2019 pour atteindre 2 millions de visiteurs ?
Pensez à écrire les nombres en chiffres pour faire le calcul facilement.
2. L'affirmation « Il y a eu environ 5 200 visiteurs par jour en 2019 » est-elle vraie ? Justifier la réponse.
Pensez à bien détailler vos calculs et vos explications.
Pensez à l'interprétation concrète de la notion de moyenne qui permet ici de trouver le calcul à réaliser pour répondre à la question posée.
Pensez à l'interprétation concrète de la notion de moyenne qui permet ici de trouver le calcul à réaliser pour répondre à la question posée.
3.
Un professeur organise une sortie pédagogique au Futuroscope pour ses élèves de troisième. Il veut répartir les 126 garçons et les 90 filles par groupes. Il souhaite que chaque groupe comporte le même nombre de filles et le même nombre de garçons.
a. Décomposer en produit de facteurs premiers les nombres 126 et 90.
La décomposition doit être justifiée avec l'écriture des calculs, mais on vous recommande de vérifier vos résultats avec la touche decomp de la calculatrice.
b. Trouver tous les entiers qui divisent à la fois les nombres 126 et 90.
Vous devez ici utiliser les décompositions obtenues à la question précédente et trouver ce qu'elles ont en commun. À partir de cela, vous pourrez en déduire les diviseurs en commun en calculant toutes les combinaisons possibles.
c. En déduire le plus grand nombre de groupes que le professeur pourra constituer. Combien de filles et de garçons y aura-t-il alors dans chaque groupe ?
Utilisez les diviseurs en commun obtenus pour trouver le plus grand nombre de groupes que le professeur peut réaliser. Pensez à bien noter tous vos calculs.
4. Deux élèves de 3e, Marie et Adrien, se souviennent avoir vu en mathématiques que les hauteurs inaccessibles pouvaient être déterminées avec l'ombre. Ils souhaitent calculer la hauteur de la Gyrotour du Futuroscope.
Marie se place comme indiquée sur la figure ci-dessous, de telle sorte que son ombre coïncide avec celle de la tour. Après avoir effectué plusieurs mesures, Adrien effectue le schéma ci-dessous (le schéma n'est pas à l'échelle), sur lequel les points A, E et B ainsi que les points A, D et C sont alignés.
Calculer la hauteur BC de la Gyrotour.
Marie se place comme indiquée sur la figure ci-dessous, de telle sorte que son ombre coïncide avec celle de la tour. Après avoir effectué plusieurs mesures, Adrien effectue le schéma ci-dessous (le schéma n'est pas à l'échelle), sur lequel les points A, E et B ainsi que les points A, D et C sont alignés.
Calculer la hauteur BC de la Gyrotour.
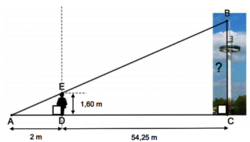 |
Vous devez reconnaître rapidement les situations classiques qui font penser aux théorèmes de Thalès et de Pythagore. Vous devez penser à justifier le parallélisme des droites pour appliquer le théorème de Thalès. Faites attention également, car les mesures données invitent à une erreur de calcul si vous ne calculez pas la longueur AC.
Corrigé
1. On sait que 1,9 million correspond à 1 900 000.
On calcule : 2 000 000 − 1 900 000 = 100 000.
Il aurait fallu 100 000 ou 0,1 million de visiteurs en plus en 2019 pour que le parc ait 2 millions de visiteurs dans l'année.
On calcule : 2 000 000 − 1 900 000 = 100 000.
Il aurait fallu 100 000 ou 0,1 million de visiteurs en plus en 2019 pour que le parc ait 2 millions de visiteurs dans l'année.
2. Pendant l'année 2019, il y a eu 365 jours, car ce n'était pas une année bissextile.
Au total, il y a eu 1 900 000 visiteurs dans cette année.
En moyenne, on a donc :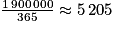 .
.
En moyenne, en 2019 il y a eu 5 205 visiteurs par jour soit environ 5 200 visiteurs.
L'affirmation est donc vraie.
Au total, il y a eu 1 900 000 visiteurs dans cette année.
En moyenne, on a donc :
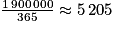 .
.En moyenne, en 2019 il y a eu 5 205 visiteurs par jour soit environ 5 200 visiteurs.
L'affirmation est donc vraie.
3.
a. On calcule : 126 = 2 × 63 = 2 × 7 × 9 = 2 × 32 × 7.
On a aussi : 90 = 2 × 45 = 2 × 5 × 9 = 2 × 32 × 5.
On a aussi : 90 = 2 × 45 = 2 × 5 × 9 = 2 × 32 × 5.
b. Dans la décomposition de 126 et 90, ces deux nombres ont en commun 2 × 32. Les diviseurs en commun pour ces deux nombres sont donc : 1 ; 2 ; 3 ; 6 (2 × 3) ; 9 (32) et 18 (2 × 32).
c. Compte tenu des diviseurs qu'ils ont en commun, on voit que le professeur pourra constituer 18 groupes au maximum avec le même nombre de filles et de garçons.
Dans chaque groupe, il y aura alors 7 garçons (126 ÷ 18 = 7) et 5 filles (90 ÷ 18 = 5).
Dans chaque groupe, il y aura alors 7 garçons (126 ÷ 18 = 7) et 5 filles (90 ÷ 18 = 5).
4. Dans cette situation, les points A, D et C et les points A, E et B sont alignés dans le même ordre. De plus, comme Marie et le Gyrotour sont supposés verticaux et donc perpendiculaires au sol, on en déduit que les droites (DE) et (CB) sont parallèles.
D'après le théorème de Thalès, on a :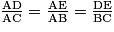 .
.
Ainsi, on obtient :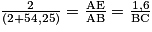 .
.
Avec un calcul de produit en croix, on a : BC = 1,6 × 56,25 ÷ 2 = 45 m.
Conclusion : la Gyrotour mesure 45 m de haut.
D'après le théorème de Thalès, on a :
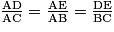 .
.Ainsi, on obtient :
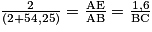 .
.Avec un calcul de produit en croix, on a : BC = 1,6 × 56,25 ÷ 2 = 45 m.
Conclusion : la Gyrotour mesure 45 m de haut.

