Énoncé
16 points
Les longueurs sont en pixels.
L'expression « s'orienter 90 » signifie que l'on s'oriente vers la droite.
On donne le programme suivant :
L'expression « s'orienter 90 » signifie que l'on s'oriente vers la droite.
On donne le programme suivant :
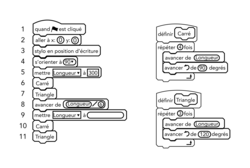 |
1. On prend comme échelle 1 cm pour 50 pixels.
a) Représenter sur votre copie la figure obtenue si le programme est exécuté jusqu'à la ligne 7 comprise.
Pour effectuer le tracé, faites attention à l'unité.
b) Quelles sont les coordonnées du stylo après l'exécution de la ligne 8 ?
Commencez par vous demander quelles sont les coordonnées du stylo avant l'exécution de la ligne 8.
2. On exécute le programme complet et on obtient la figure ci-dessous qui possède un axe de symétrie vertical.
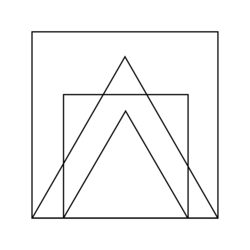 |
Recopier et compléter la ligne 9 du programme pour obtenir cette figure.
Il s'agit de déterminer la valeur mise dans la variable « Longueur » à la ligne 9.
3.
a) Parmi les transformations suivantes, translation, homothétie, rotation, symétrie axiale, quelle est la transformation géométrique qui permet d'obtenir le petit carré à partir du grand carré ? Préciser le rapport de réduction.
Vous pouvez commencer par exclure les transformations géométriques qui conservent les longueurs, car ce n'est pas le cas ici.
b) Quel est le rapport des aires entre les deux carrés dessinés ?
Rappelez-vous qu'une réduction de rapport k multiplie les aires par k2.
Corrigé
1.
a) L'échelle étant de 1 cm pour 50 pixels, on obtient la figure ci-dessous qui est composée d'un carré et d'un triangle équilatéral, chacun de 6 cm de côté.
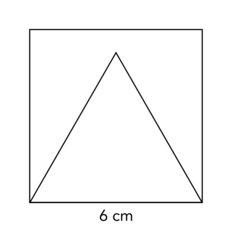 |
b) Avant l'exécution de la ligne 8, les coordonnées du stylo sont (0 ; 0), car il est revenu à la position de départ.
La valeur « longueur / 6 » est égale à 300 ÷ 6 = 50.
Le stylo se déplacant vers la droite, ses coordonnées après l'exécution de la ligne 8 sont (50 ; 0).
La valeur « longueur / 6 » est égale à 300 ÷ 6 = 50.
Le stylo se déplacant vers la droite, ses coordonnées après l'exécution de la ligne 8 sont (50 ; 0).
2. La figure obtenue en exécutant le programme complet possède un axe de symétrie vertical. On peut compléter la figure des mesures ci-dessous.
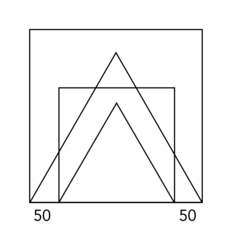 |
De la figure complétée, on déduit que la valeur mise dans la variable « Longueur » à la ligne 9 est 300 − 2 × 50 = 300 − 100 = 200.
3.
a) La longueur du côté du petit carré n'est pas la même que la longueur du côté du grand carré.
Or, une translation, une rotation ou une symétrie axiale sont des transformations géométriques qui conservent les longueurs donc elles ne conviennent pas.
La transformation géométrique qui convient est donc l'homothétie et c'est celle de centre le milieu des côtés des deux carrés qui a pour coordonnées (150 ; 0).
Le rapport de réduction est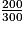 =
= 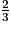 .
.
Or, une translation, une rotation ou une symétrie axiale sont des transformations géométriques qui conservent les longueurs donc elles ne conviennent pas.
La transformation géométrique qui convient est donc l'homothétie et c'est celle de centre le milieu des côtés des deux carrés qui a pour coordonnées (150 ; 0).
Le rapport de réduction est
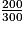 =
= 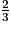 .
.b) Une réduction de rapport k multiplie les aires par k2.
Le rapport de réduction de l'homothétie est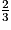 donc le rapport des aires entre les deux carrés dessinés est
donc le rapport des aires entre les deux carrés dessinés est 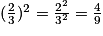 .
.
Le rapport de réduction de l'homothétie est
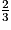 donc le rapport des aires entre les deux carrés dessinés est
donc le rapport des aires entre les deux carrés dessinés est 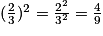 .
.
