Énoncé
8 points
Document 1
Le surpoids est devenu un problème majeur de santé, celui-ci prédispose à beaucoup de maladies et diminue l'espérance de vie.
L'indice le plus couramment utilisé est celui de masse corporelle (IMC).
Le surpoids est devenu un problème majeur de santé, celui-ci prédispose à beaucoup de maladies et diminue l'espérance de vie.
L'indice le plus couramment utilisé est celui de masse corporelle (IMC).
Document 2
L'IMC est une grandeur internationale permettant de déterminer la corpulence d'une personne adulte entre 18 ans et 65 ans.
Il se calcule avec la formule suivante :
IMC =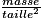
avec « masse » en kg et « taille » en m.
Normes :
L'IMC est une grandeur internationale permettant de déterminer la corpulence d'une personne adulte entre 18 ans et 65 ans.
Il se calcule avec la formule suivante :
IMC =
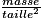
avec « masse » en kg et « taille » en m.
Normes :
- 18,5
 IMC < 25 : corpulence normale ;
IMC < 25 : corpulence normale ; - 25
 IMC < 30 : surpoids ;
IMC < 30 : surpoids ; - IMC
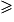 30 : obésité.
30 : obésité.
1.
Dans une entreprise, lors d'une visite médicale, un médecin calcule l'IMC de six des employés. Il utilise pour cela une feuille de tableur dont voici un extrait :
 |
a)
Combien d'employés sont en situation de surpoids ou d'obésité dans cette entreprise ?
Rappelez-vous qu'une personne est en situation de surpoids ou d'obésité lorsque son IMC est supérieur ou égal à 25.
b)
Laquelle de ces formules a-t-on écrite dans la cellule B3, puis recopiée à droite, pour calculer l'IMC ?
Recopier la formule correcte sur la copie.
Recopier la formule correcte sur la copie.
 |
Observez la formule de l'IMC et les cases où sont situées les masses et les tailles.
2.
Le médecin a fait le bilan de l'IMC de chacun des 41 employés de cette entreprise. Il a reporté les informations recueillies dans le tableau suivant dans lequel les IMC ont été arrondis à l'unité près.
| IMC | 20 | 22 | 23 | 24 | 25 | 29 | 30 | 33 | Total |
| Effectif | 9 | 12 | 6 | 8 | 2 | 1 | 1 | 2 | 41 |
a)
Calculer une valeur approchée, arrondie à l'entier près, de l'IMC moyen des employés de cette entreprise.
N'oubliez pas de pondérer chaque valeur de l'IMC par son effectif.
b)
Quel est l'IMC médian ? Interpréter ce résultat.
Rappelle-toi que la médiane d'une série statistique est une valeur qui partage cette série en deux groupes d'effectifs égaux : 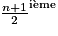 des valeurs classées par ordre croissant.
des valeurs classées par ordre croissant.
- un groupe constitué de valeurs inférieures ou égales à la médiane ;
- un groupe constitué de valeurs supérieures ou égales à la médiane.
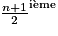 des valeurs classées par ordre croissant.
des valeurs classées par ordre croissant.c)
On lit sur certains magazines : « On estime qu'au moins 5 % de la population mondiale est en surpoids ou est obèse. » Est-ce le cas pour les employés de cette entreprise ?
Rappelez-vous qu'une personne est en situation de surpoids ou d'obésité lorsque son IMC est supérieur ou égal à 25.
Corrigé
1.
a)
D'après l'énoncé, une personne est en situation de surpoids ou d'obésité lorsque son IMC est supérieur ou égal à 25.
D'après la feuille du tableur, trois personnes sont dans une situation de surpoids ou d'obésité : celles qui ont respectivement pour IMC 25,2 ; 28,7 et 33,2.
D'après la feuille du tableur, trois personnes sont dans une situation de surpoids ou d'obésité : celles qui ont respectivement pour IMC 25,2 ; 28,7 et 33,2.
b)
D'après l'énoncé, on a : IMC = 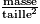 .
.
Pour calculer B3, on utilise la masse qui est notée dans la case B2 et la taille (au carré) qui est notée dans la case B1.
Comme les colonnes ne sont pas bloquées, la formule qu'il faut écrire dans la cellule B3, puis recopiée à droite, est : « = B2/(B1*B1) ».
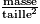 .
.Pour calculer B3, on utilise la masse qui est notée dans la case B2 et la taille (au carré) qui est notée dans la case B1.
Comme les colonnes ne sont pas bloquées, la formule qu'il faut écrire dans la cellule B3, puis recopiée à droite, est : « = B2/(B1*B1) ».
2.
a)
L'IMC moyen des employés de cette entreprise est :
M =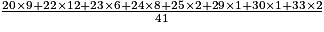
M =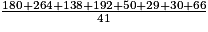
M =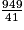
M 23 à l'entier près.
23 à l'entier près.
L'IMC moyen des employés de cette entreprise est d'environ 23.
M =
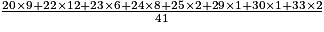
M =
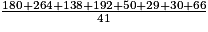
M =
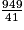
M
 23 à l'entier près.
23 à l'entier près.L'IMC moyen des employés de cette entreprise est d'environ 23.
b)
L'effectif de la série est un nombre impair.
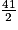 = 20,5 donc la médiane de cette série statistique est la 21e des valeurs classées par ordre croissant.
= 20,5 donc la médiane de cette série statistique est la 21e des valeurs classées par ordre croissant.
D'après le tableau, l'IMC médian des employés de cette entreprise est 22.
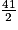 = 20,5 donc la médiane de cette série statistique est la 21e des valeurs classées par ordre croissant.
= 20,5 donc la médiane de cette série statistique est la 21e des valeurs classées par ordre croissant.D'après le tableau, l'IMC médian des employés de cette entreprise est 22.
c)
Dans cette entreprise, 6 employés sur 41 sont en situation de surpoids ou d'obésité.
Le pourcentage d'employés en situation de surpoids ou d'obésité dans cette entreprise est de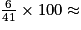 14,6 % au dixième près.
14,6 % au dixième près.
L'affirmation « On estime qu'au moins 5 % de la population mondiale est en surpoids ou est obèse » est donc vraie pour cette entreprise.
Le pourcentage d'employés en situation de surpoids ou d'obésité dans cette entreprise est de
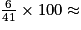 14,6 % au dixième près.
14,6 % au dixième près.L'affirmation « On estime qu'au moins 5 % de la population mondiale est en surpoids ou est obèse » est donc vraie pour cette entreprise.

